Алгоритм Kosaraju по полкам

На самом деле, уже есть статья на Хабре по этому алгоритму, но она не освещает доказательство корректности и некоторых шагов алгоритма. Я решил создать более справочную версию той статьи с полным разбором.

Этот пост будет полезен студентам, изучающим дисциплину “Алгоритмы и Теория графов”, а также тем, кто хочет улучшить/освежить свои знания об алгоритмах на графах.

Для того, чтобы понять алгоритм Косарайю необходимо владеть некоторыми понятиями теории графов

Основные понятия

Вершины u, v называются сильно связными, если в графе G существует путь (необязательно прямой) u→v И v→u (Обозначим сильно связные вершины u↔v)

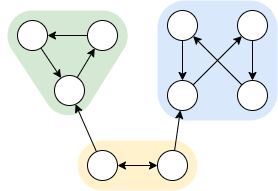
Компоненты сильной связности – максимальные по включению сильно связные подграфы.

Инвертирование графа — смена направления всех рёбер в графе на противоположные (двунаправленное ребро остаётся самим собой)

Инвертирование графа – процесс поворота рёбер в обратную сторону (двунаправленное ребро останется самим собой)

Можно привести несколько достаточно очевидных лемм:

1. Компонента сильной связности — это множество вершин, входящих в множество циклов,
имеющих хотя бы одну общую вершину

2. Инвертирование рёбер цикла не влияет на его цикличность

3. Если истинно u ↔ v И v ↔ w, то истинно u ↔ v ↔ w

4. Отдельная вершина представляет собой одну компоненту сильной связности

Алгоритм непосредственно

Алгоритм предназначен для поиска компонент сильной связности в ориентированном графе и состоит из трёх шагов:

1. Выполнить поиск в глубину (DFS), пока не будут «помечены» все вершины. Вершина считается «помеченной», когда ей присвоен индекс в порядке завершения рекурсивных шагов тактов DFS  (время выхода).

   Назовём одним тактом DFS поиск очередного дерева путей 

2. Инвертировать исходный граф

3. Выполнить DFS в порядке убывания пометок вершин.

Полученные деревья каждого такта DFS последнего шага являются компонентами сильной связности

Небольшое, но важное уточнение: время выхода следует считать следующим образом: изначально счётчик времени нулевой, а увеличивается он в двух случаях:

1. Начало нового такта DFS

2. Прохождение по ребру (при том, не важно, рекурсивный проход или нет)

Прежде чем доказывать алгоритм, предлагаю разобрать пример работы алгоритма

Пример работы алгоритма Косарайю пошагово

Дан следующий граф:

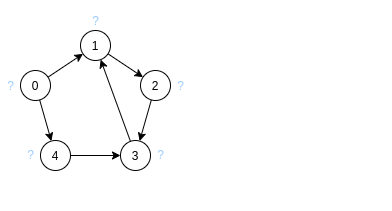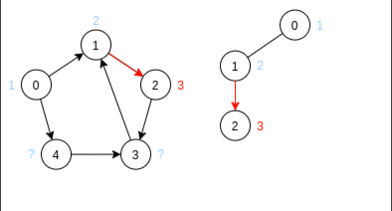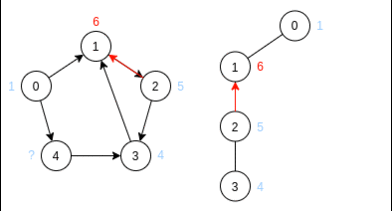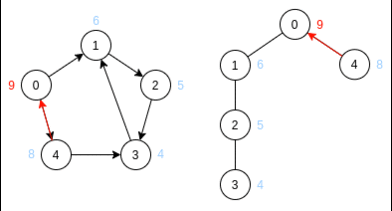
Шаг 1:
Непомеченные вершины имеют метку ‘?’
Справа от исходного графа находится дерево DFS (если была возможность выбрать из 2 рёбер, я выбирал пойти в вершину с меньшим индексом; можете проверить сами, как работает алгоритм, если выбирать бОльший индекс)

Из иллюстрации видно, как работает рекурсия алгоритма поиска в глубину – возвращаясь из вершины (из которой больше нет путей в непомеченные вершины) время увеличивается на 1

Из этого шага прослеживается, что вершина начала такта (корень) имеет самую большую (в такте) метку — это объясняется рекурсивностью алгоритма DFS — алгоритм заходит в одну вершину и выходит из неё же. Этот факт понадобится при доказательстве

Шаг 2:
Инвертируем рёбра

Шаг 3:
Так как теперь нам интересен лишь лес тактов DFS, то нет смысла считать время выхода из вершин, поэтому я не показал рекурсивных переходов

Справа от инвертированного графа
показан лес тактов DFS

После завершения алгоритма имеем 3 компоненты сильной связности

Доказательство корректности алгоритма

Немного уточним, что требуется доказать:

Вершины u и v сильно связны ⇔ после выполнения алгоритма они принадлежат одному дереву такта DFS

Доказательство:
⇒
Если вершины u и v были сильно связны в графе G, то на третьем этапе будет найден путь из одной вершины в другую (по лемме 2), это означает, что по окончании алгоритма обе вершины лежат в одном дереве.
⇐

Вершины u и v лежат в одном и том же дереве поиска в глубину на третьем шаге алгоритма. Значит, они обе достижимы из корня r этого дерева.

Вершина r была рассмотрена на 3 шаге раньше всех, значит время выхода из неё на 1 шаге больше, чем время выхода из вершин u и v. Из этого мы получаем 2 случая:

1. Обе эти вершины были достижимы из r в исходном графе. Это означает сильную связность вершин u и r и сильную связность вершин v и r (по лемме 2). Складывая пути мы получаем связность вершин u и v (по лемме 3)

2. Хотя бы одна вершина не достижима из r в исходном графе, например v. Значит и r была не достижима из v в исходном графе, так как время выхода r — больше (если бы она была достижима, то время выхода v было бы больше, чем у r, просмотрите ещё раз первый шаг примера). Значит между этими вершинами нет пути (ни в исходном, ни в инвертированном графах), но последнего быть не может, потому что по условию v достижима из r на 3 шаге (в инвертированном графе)

Значит, из случая 1 и не существования случая 2 получаем, что вершины u и v сильно связны в обоих графах

Сложность алгоритма

Поиск в глубину в исходном графе выполняется за O(V+E)

Для того, чтобы инвертировать все ребра в графе, представленном в виде списка смежности потребуется O(V+E) действий. Для матричного представления графа не нужно выполнять никакие действия для его инвертирования (индексы столбцов будут использоваться в качестве индексов строк и наоборот)

Количество рёбер в инвертированном равно количеству рёбер в изначальном графе, поэтому поиск в глубину будет работать за O(V+E)

В итоге получаем, что сложность алгоритма — O(V+E)

Итог

Алгоритм Косарайю ищет компоненты сильной связности, причём делает он это за O(V+E) времени.

Где применять алгоритм, полностью зависит от Вашего воображения составлять графы.

Например: проецирование транспортной сети на граф. Алгоритм поможет проверить новоиспечённую транспортную сеть на достижимость каждой вершины из каждой вершины (чтобы убедиться, что есть путь из окраины в центр и обратно).

Можно тестировать алгоритмом систему воздуховода в зданиях; течение тока в полупроводниковых приборах

Можно мыслить шире: проецируем кровеносную систему живого существа, которое Вам поручили создать в рамках проекта генной инженерии, где-нибудь в 2077 году). Алгоритм поможет узнать, доходит ли кровь от сердца до органов и обратно.