Визуальное представление разложения числа на множители с помощью тригонометрических функций

Возьмём гиперболу вида:

Здесь n – число, делители которого должны быть найдены. Умножим f(x) на cos[π⋅f(x)] (прим. – скобки ( ) и [ ] равнозначны и не вносят дополнительных смыслов). И возьмём модуль полученной функции g(x):

Графики f(x) и |g(x)| показаны на рис. 1. n при этом взято равным 15. И это один из главных недостатков метода, при больших значениях n аргумент косинуса меняется с очень высокой частотой.

Если возвести в четную степень косинус, получим график, изображённый на рисунке 2 красным.

На последнем шаге “профильтруем” (см. рис. 3) наш косинус (т.е. умножим g(x)) функцией вида [sin(π⋅x/20)⋅sin(3π⋅x/20)⋅sin(5π⋅x/20)⋅sin(7π⋅x/20)]^20.

На графике будут видны все возможные делители числа n. В нашем случае это 1, 3, 5, 15.

Если взять n=105, на рисунках 4, 5 можно увидеть возможные делители 1, 3, 5, 7, 15, 21, 35. 105 не показано.

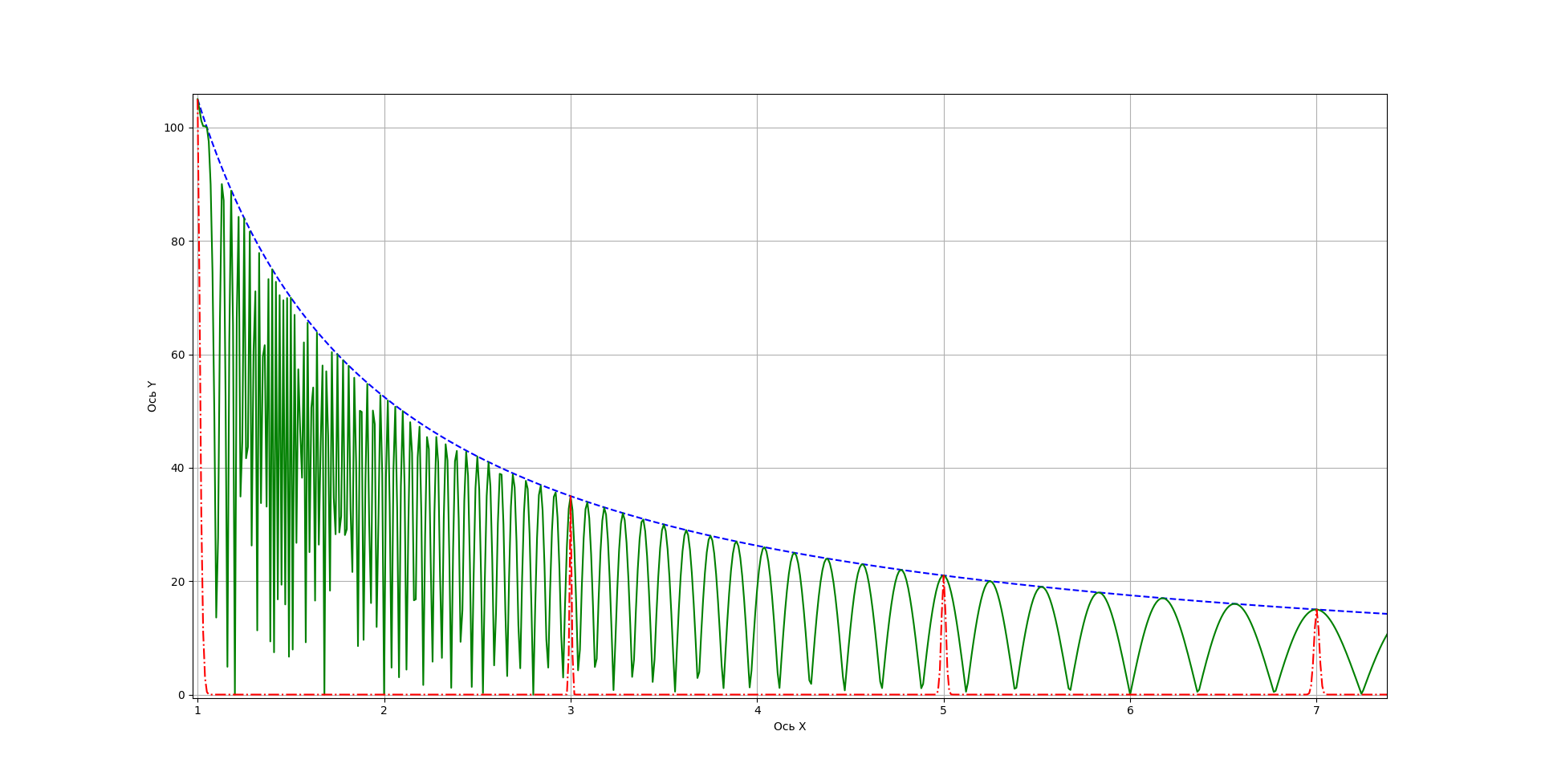
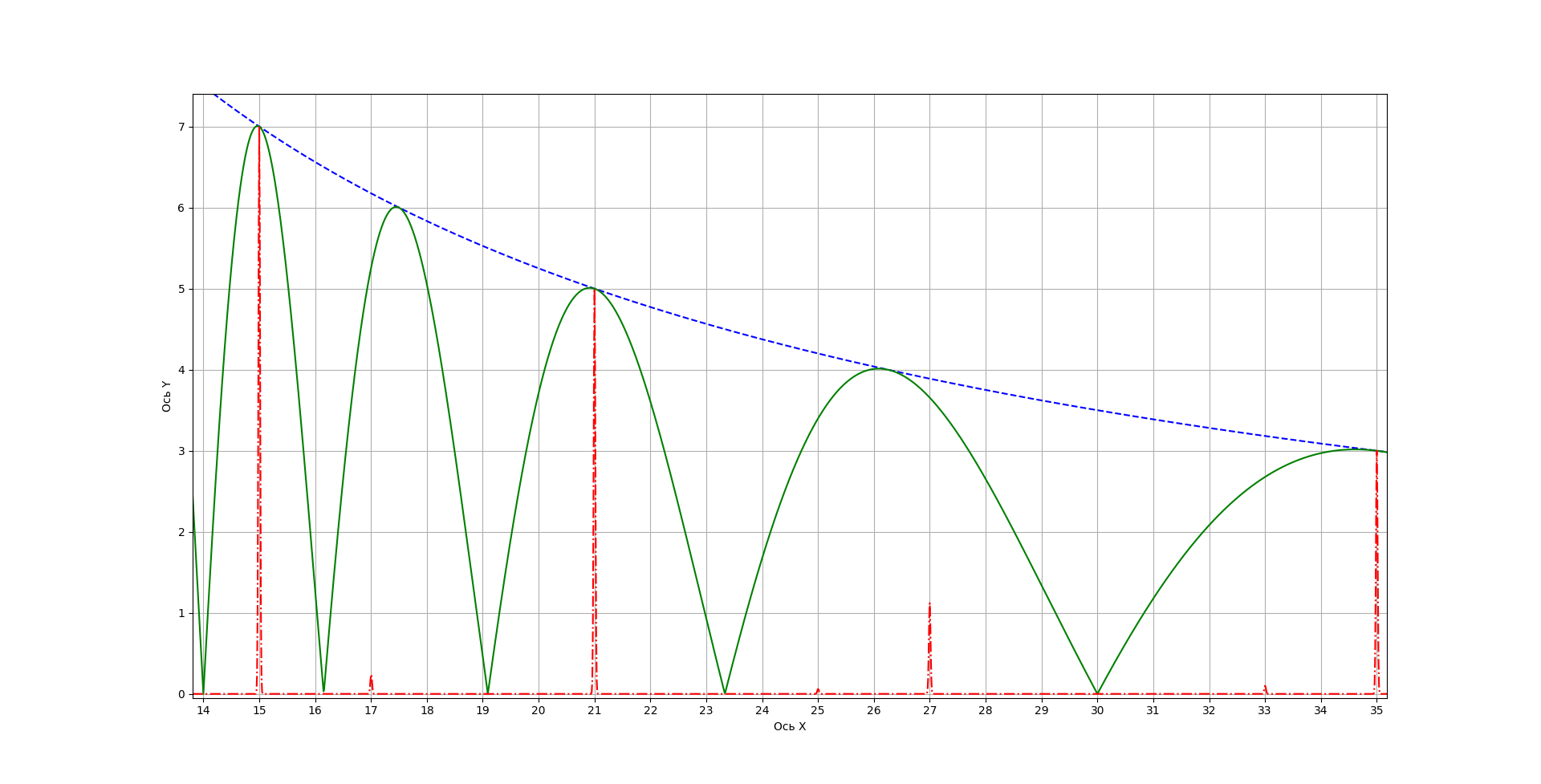
“Поиграв” степенями и аргументами синусов, можно добиться необходимой для конкретной задачи картины.

Т.к. гиперболой описывается изотермический процесс, позаимствовав из термодинамики p-V-T диаграмму, изложенное выше можно представить и в трёхмерном виде. Для красоты на рис. 6 все множители нормированы по величине 10.

Некоторые справочные данные функции (-cos[π⋅f(x)]) :

1. Количество периодов на отрезке от 1 до n равно N_n=(n-1)/2

2. Номер периода N для координаты x можно вычислить по формуле N_x=n⋅(x-1)/2⋅x

3. Координата х N-го периода вычисляется по формуле x_N=n/(n-2⋅N)

4. Отношение значения координаты x_N+1 к x_N: x_N+1/x_N=1+2/(n-2⋅N)

5. Если представить число достаточно большое n как произведение П(1+2/(n-2⋅N)) от 1 до N_n, первые ≈63,2% членов при произведении дадут число е.