Как сделать ёлку, если ты математик #2

Продолжение вчерашней статьи, посвящённой fЁлке, ниже.

Базовые функции

Трапеция

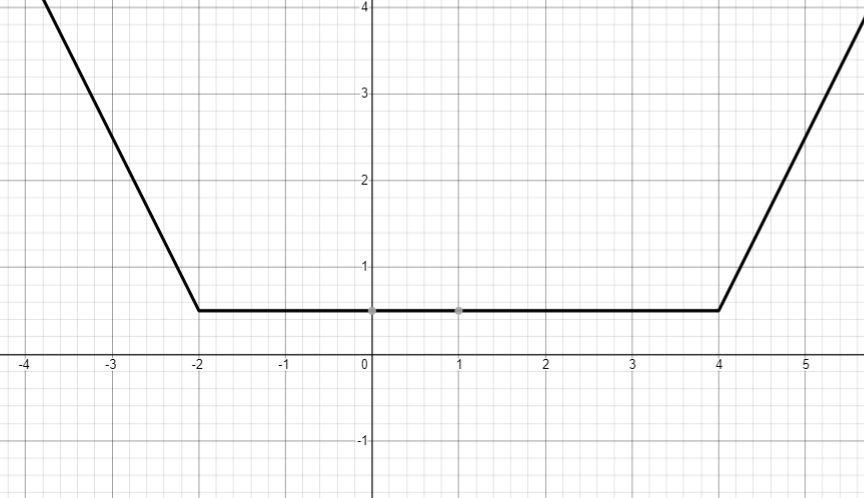
Здесь дважды применяется модуль числа, меняя константы под модулем и вычитаемое мы можем регулировать длину отрезка с константным значением y и само значение y на данном отрезке. Данная функция позже пригодится для сугробов и ведра.

Альтернативный эллипс

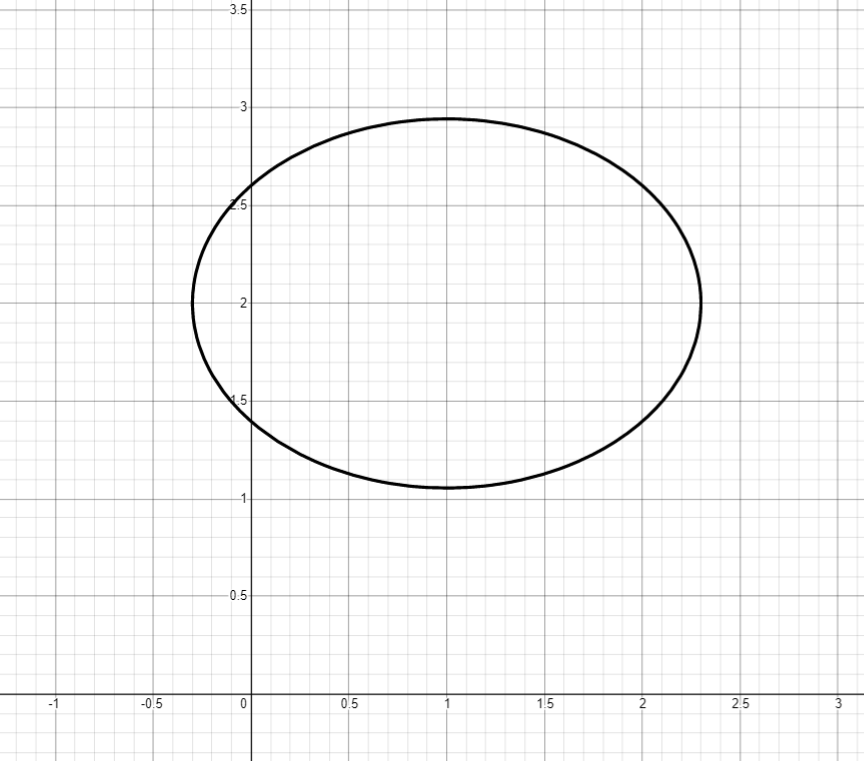
$sqrt{left(x-1right)^{2}+1.9left(y-2right)^{2}}-1.3=0$

Альтернативная запись эллипса. Константы внутри скобок отвечают за координаты центра эллипса, константы перед скобками – за степень сжатия по осям, число за корнем – радиус.

Эллипс по двум точкам

$sqrt{left(x-1right)^{2}+left(y-2right)^{2}}+sqrt{left(x-0.1right)^{2}+left(y+1right)^{2}}-3.3=0$

Согласно определению, эллипс – это замкнутая кривая, сумма расстояний каждой точки которой до двух точек (A и B на изображении) равна постоянной величине. Данный тип эллипса пригодится для рисования рук снеговику.

Прямоугольник

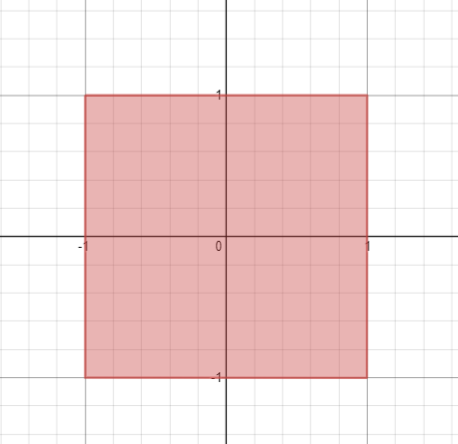
Это такая фигура, максимальное расстояние от точек которой до осей координат не превышает константного значения.

Если размер прямоугольника одинаков – его можно вынести за знак сравнения:

Снеговик

Тело – три эллипса

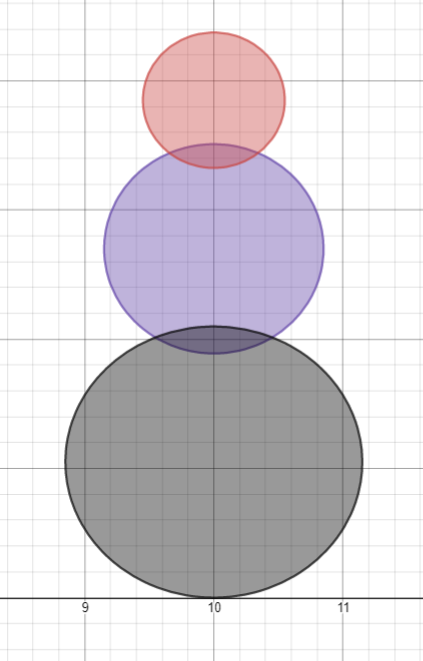
$s_{1}=sqrt{left(x-10right)^{2}+1.1left(y-3.85right)^{2}}-0.55$ $s_{2}=sqrt{left(x-10right)^{2}+1.1left(y-2.7right)^{2}}-0.85$ $s_{3}=sqrt{left(x-10right)^{2}+1.2left(y-1.05right)^{2}}-1.15$

Объединение снеговика – операция min ко всем эллипсам.

$minleft(s_{1}, s_{2},s_{3}right)le0$

Ведро на голову!

Шаг первый – трапеция

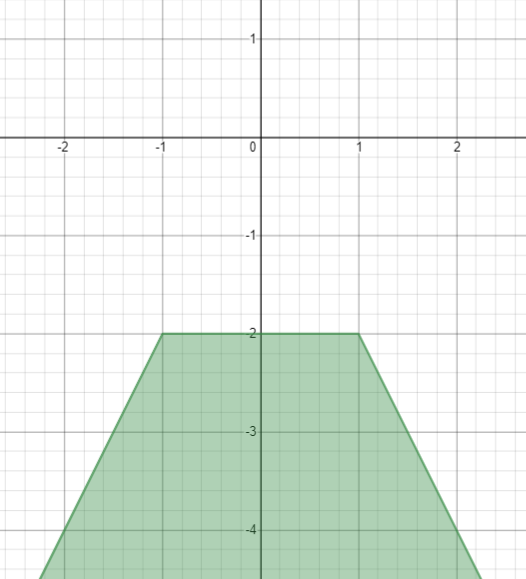
Шаг второй – доработаем форму, поднимем ведро

Для того, чтобы поднять ведро – добавляем 2 в начало, чтобы стенки ведра стали более крутыми – поставим множители перед модулями.

Шаг третий – ограничение снизу

Применим схожую методику, как делали это с ёлкой.

Черный график:

$x=frac{left(left|yright|+yright)}{2}$

Красный график

$x=frac{100left(left|yright|-yright)}{2}$

Суммируем, получаем ограничитель для ведра

$x=left(frac{left(left|yright|+yright)}{2}+frac{100left(left|yright|-yright)}{2}right)$

Применяем – ведро готово

$2-1.9left|x-0.3right|-1.9left|x+0.3right|-left(frac{left(left|yright|+yright)}{2}+frac{100left(left|yright|-yright)}{2}right)ge0$

Шаг пятый – наденем ведро на голову

Переместим

$2-1.9left|x-9.7right|-1.9left|x-10.3right|-left(frac{left(left|y-4right|+y-4right)}{2}+frac{100left(left|y-4right|-y+4right)}{2}right)ge0$

Объединим со снеговиком

$s_{4}=2-1.9left|x-9.7right|-1.9left|x-10.3right|-left(frac{left(left|y-4right|+y-4right)}{2}+frac{100left(left|y-4right|-y+4right)}{2}right)$ $minleft(s_{1}, s_{2},s_{3},-s_{4}right)le0$

Здесь минус перед s₄ по той причине, что для получения ведра использовалось сравнение >0, вместо <0, когда велась работа с эллипсами.

Руки – эллипсы

Ось симметрии снеговика – это x = 10, поэтому можно создать две руки, а позже глаза и рот, одной функцией.

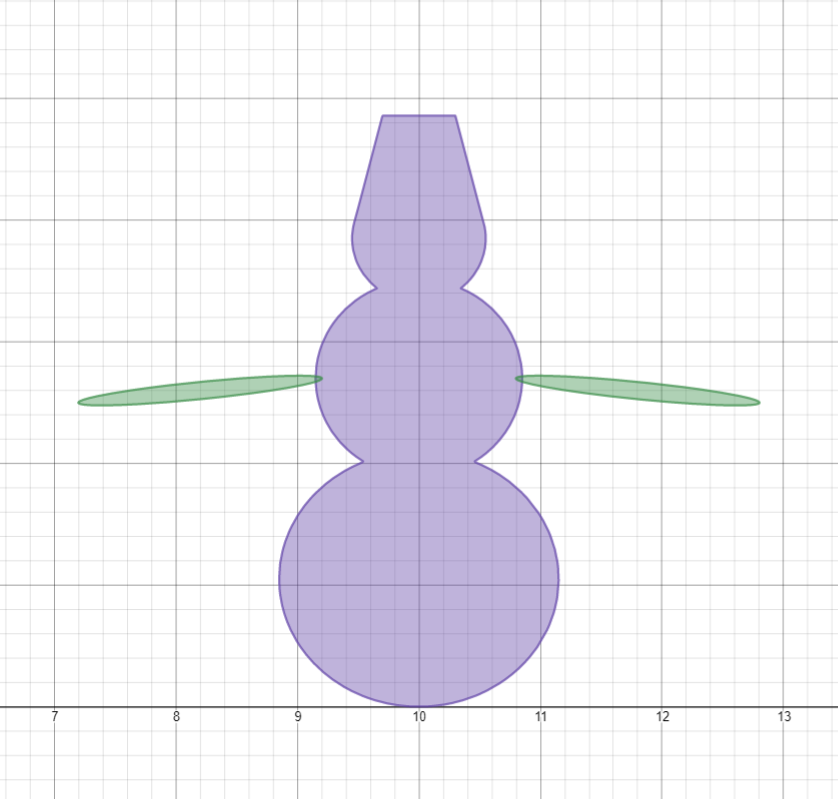
$h_{1}=sqrt{left(left|x-10right| - 0.8right)^{2}+left(y-2.7right)^{2}}+sqrt{left(left|x-10right| - 2.8right)^{2}+left(y-2.5right)^{2}}-2.015\h_1le0$

Пальцы аналогично, но симметрия не только по х = 10, но и у = 2.55

$h_{2}=sqrt{left(left|x-10right| - 1.9right)^{2}+left(y-2.55right)^{2}}+sqrt{left(left|x-10right| - 2.3right)^{2}+left(left|y-2.55right|-0.3right)^{2}}-0.51\h_2le0$

Тело снеговика по элементам

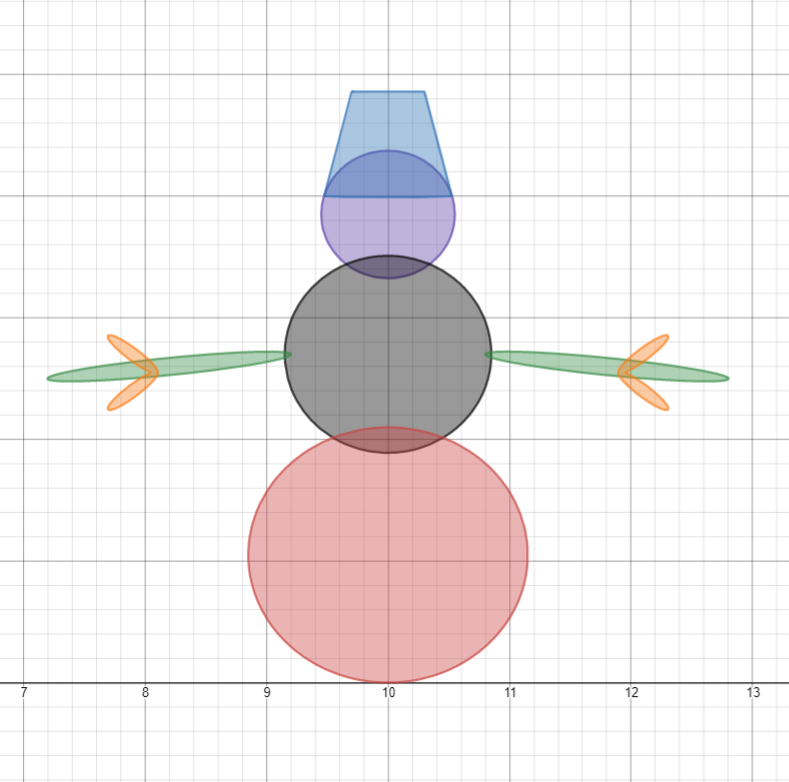
Результат тела снеговика

$minleft(s_{1}, s_{2},s_{3},-s_{4},h_{1},h_{2}right)le0$

Лицо

Глаза – 2 круга

$100left(left|x-10right|-0.2right)^{2}+100left(y-3.95right)^{2}le1$

Рот – два эллипса

$left(300left(left|x-10right|-0.03-0.-left(y-3.6right)right)^{2}+3000left(y-3.6right)^{2}right)le1$

Все функции снеговика для вставки в desmos

s_{1}=sqrt{left(x-10right)^{2}+1.1left(y-2.7right)^{2}}-0.85

s_{2}=sqrt{left(x-10right)^{2}+1.2left(y-1.05right)^{2}}-1.15

s_{3}=sqrt{left(x-10right)^{2}+1.1left(y-3.85right)^{2}}-0.55

s_{4}=2-1.9left|x-9.7right|-1.9left|x-10.3right|-left(frac{left(left|y-4right|+y-4right)}{2}+frac{100left(left|y-4right|-y+4right)}{2}right)

h_{1}=sqrt{left(left|x-10right| – 0.8right)^{2}+left(y-2.7right)^{2}}+sqrt{left(left|x-10right| – 2.8right)^{2}+left(y-2.5right)^{2}}-2.015

h_{2}=sqrt{left(left|x-10right| – 1.9right)^{2}+left(y-2.55right)^{2}}+sqrt{left(left|x-10right| – 2.3right)^{2}+left(left|y-2.55right|-0.3right)^{2}}-0.51

minleft(s_{1}, s_{2},s_{3},-s_{4},h_{1},h_{2}right)le0

100left(left|x-10right|-0.2right)^{2}+100left(y-3.95right)^{2}le1

left(300left(left|x-10right|-0.03-0.-left(y-3.6right)right)^{2}+3000left(y-3.6right)^{2}right)le1

Сугробы

Сугробы – функция модуля синуса с константной частотой и изменяемой амплитудой. Амплитуду будем регулировать с помощью трапеций.

$d_{1}=-left|x+7right|-left|x-14right|+22\d_{2}=left|x+2.7right|+left|x-2.7right|-6.35\d_{3}=left|x-9right|+left|x-11right|-2.8$

Суммируем

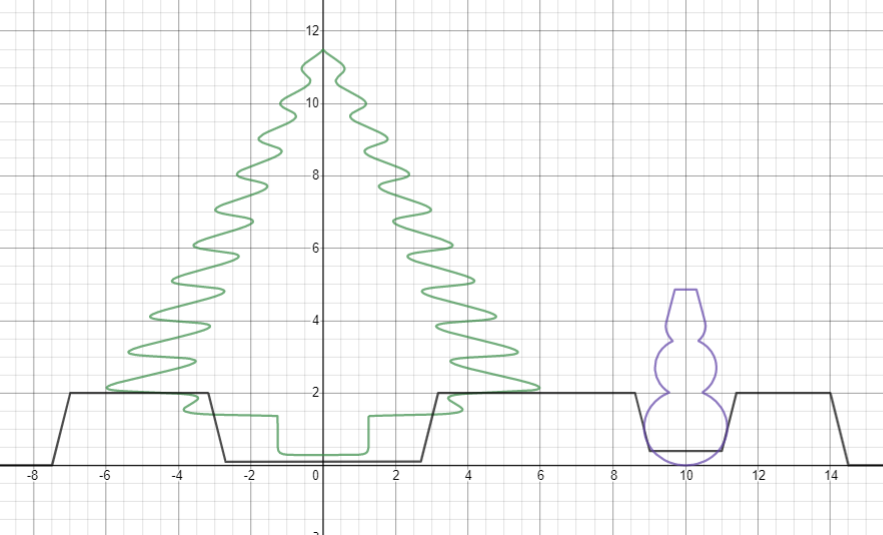
$d=d_{1}+left|d_{1}right|+d_{2}-left|d_{2}right|+d_{3}-left|d_{3}right|$

Результат

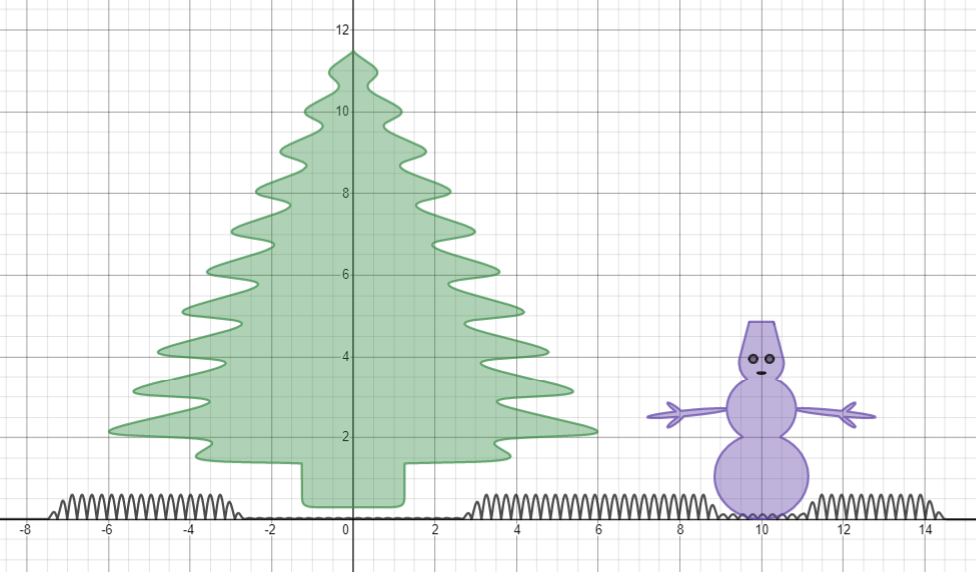
Все функции сугробов

d_{1}=-left|x+7right|-left|x-14right|+22

d_{2}=left|x+2.7right|+left|x-2.7right|-6.35

d_{3}=left|x-9right|+left|x-11right|-2.8

d=d_{1}+left|d_{1}right|+d_{2}-left|d_{2}right|+d_{3}-left|d_{3}right|

0.3dleft|sinleft(13xright)right|

Снежинки

Всё предельно просто. Снежинка – это “окружность наоборот”, вместо второй степени используется корень, а для того, чтобы он вычислялся используются модули x и у.

Много снежинок

Используем mod, остаток от деления

Результат

$f_{1}=sqrt{left|operatorname{mod}left(x,2right)-1right|}+sqrt{left|operatorname{mod}left(y,2right)-1right|}-0.45\f_1le0$

Корректировка снежинок

Снежинки закрывают ёлку и снеговика, исправим это с помощью эллипсов.

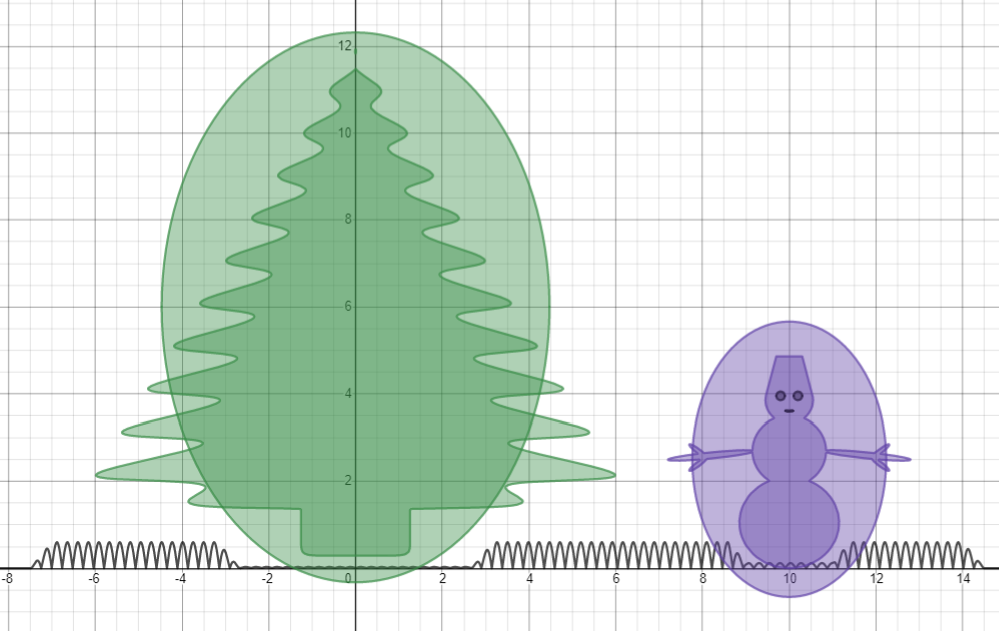
$f_{2}=2xx+left(y-6right)^{2}-40\f_{3}=2left(x-10right)^{2}+left(y-2.5right)^{2}-10\f_2le0\f_3le0$

Комбинируем

$minleft(-f_{1},f_{2},f_{3}right)ge0$

Все формулы снежинок

f_{1}=sqrt{left|operatorname{mod}left(x,2right)-1right|}+sqrt{left|operatorname{mod}left(y,2right)-1right|}-0.45

f_{2}=2xx+left(y-6right)^{2}-40

f_{3}=2left(x-10right)^{2}+left(y-2.5right)^{2}-10

minleft(-f_{1},f_{2},f_{3}right)ge0

Подарки под ёлку

Подарок – это квадрат. Подарков будет два, поэтому используя |x| будем рисовать сразу два подарка и сразу два бантика к ним.

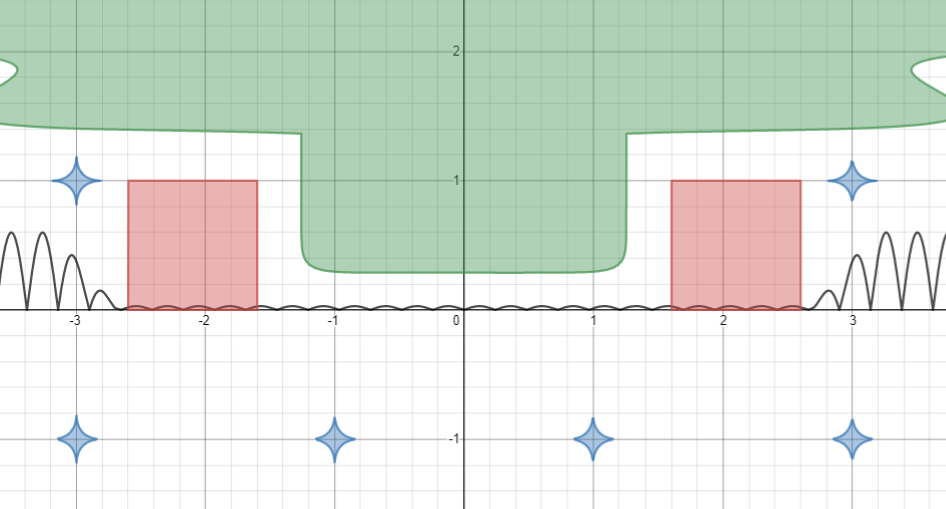
Формула

Бантики к подаркам

Модуль

$j_{1}=left|0.9left|left|xright|-2.1right|right|-left(y-1right)-0.2\j_1le0$

Гипербола

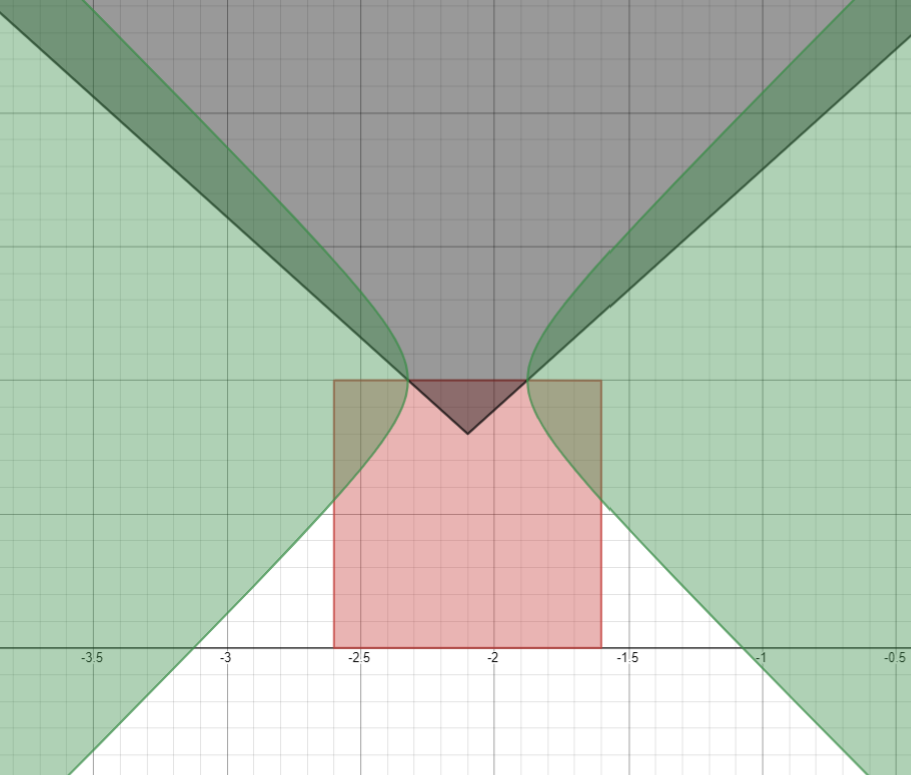
$j_{2}=left|left|xright|-2.1right|^{2}-left(y-1right)^{2}-0.05\j_2ge0$

Круг

$j_{3}=0.2left|left|xright|-2.1right|^{2}+0.2left(y-1right)^{2}-0.1\j_3le0$

Эллипс

$j_{4}=left(0.5left|left|xright|-2.1right|right)^{2}+left(y-1right)^{2}-0.02\j_4le0$

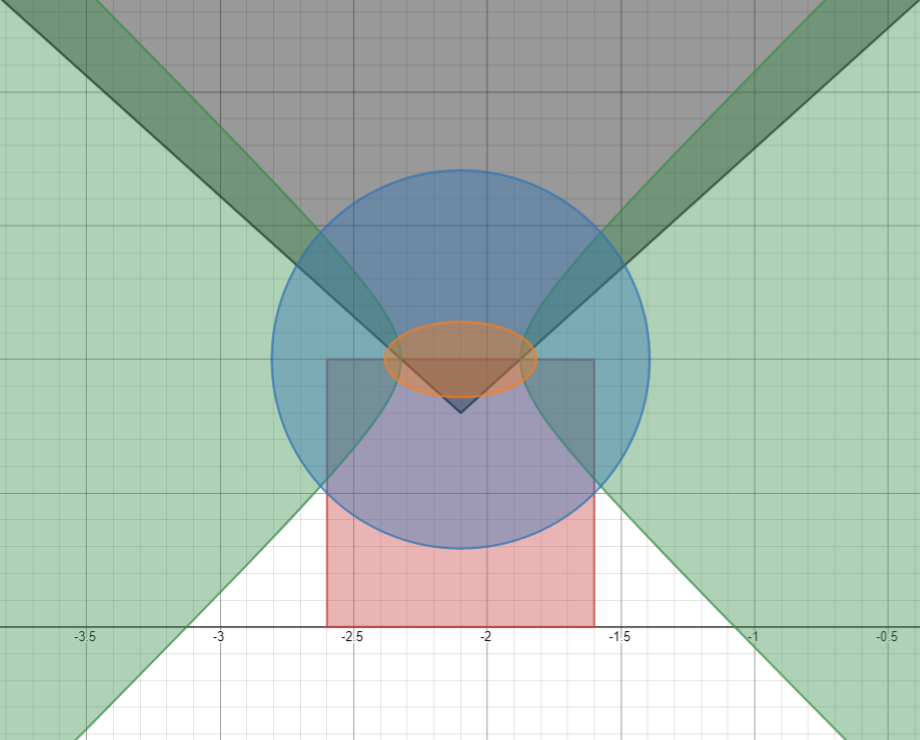
Внезапный ход: множим эллипс на модуль

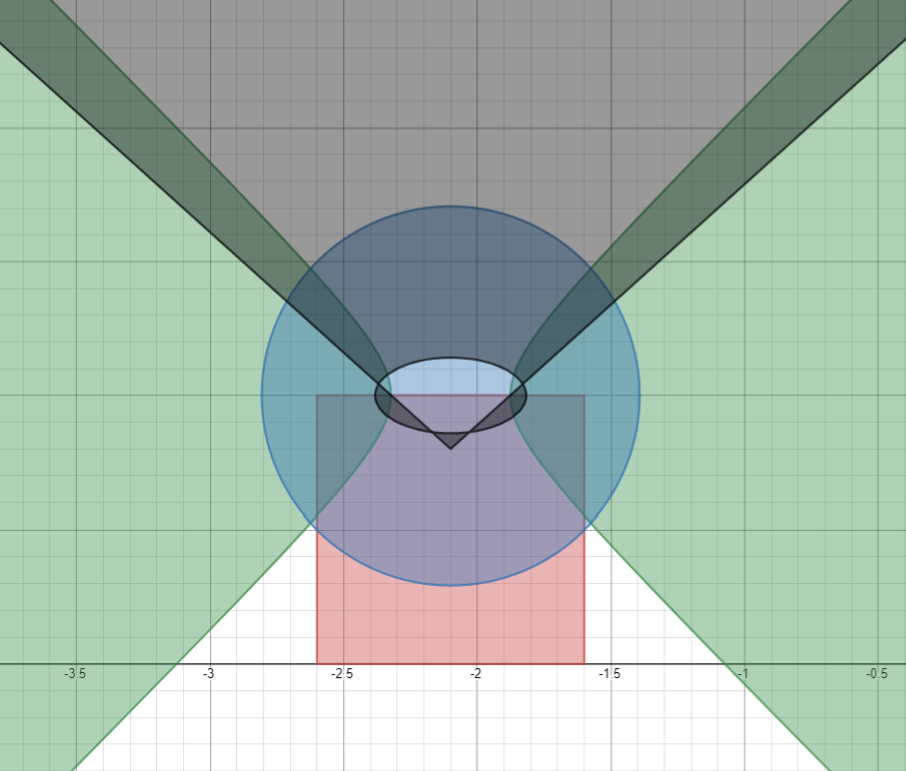
Комбинируем все элементы

$maxleft(j_{1}j_{4}, -j_{2}, j_{3}right)le0$

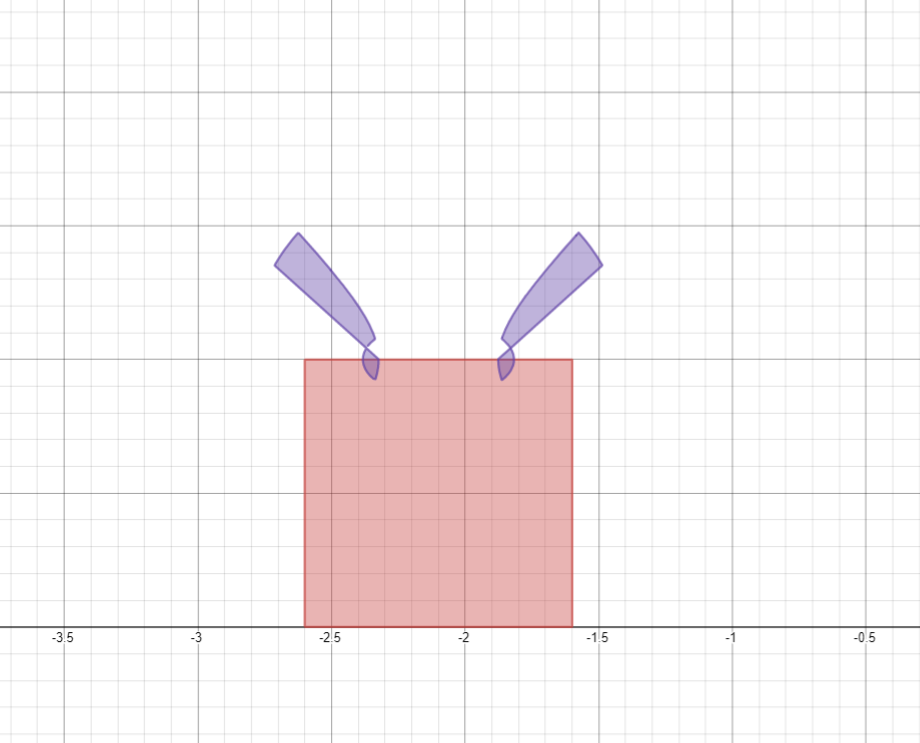
Все формулы для бантиков

j_{1}=left|0.9left|left|xright|-2.1right|right|-left(y-1right)-0.2

j_{2}=left|left|xright|-2.1right|^{2}-left(y-1right)^{2}-0.05

j_{3}=0.2left|left|xright|-2.1right|^{2}+0.2left(y-1right)^{2}-0.1

j_{4}=left(0.5left|left|xright|-2.1right|right)^{2}+left(y-1right)^{2}-0.02

maxleft(j_{1}j_{4}, -j_{2}, j_{3}right)le0

Цифры

Для начала зададим локальную систему координат, это будет полезно, когда мы будем двигать надпись.

$x_{1}=x\y_{1}=y$

2021 в римской системе счисления будет MMXXI, это несколько упрощает задачу

Две буквы “М”

Определим для начала функцию t2, которая будет ограничивать каждую букву М

$t_{2}=maxleft(left|left|x_{1}right|-1right|,left|y_{1}-0.89right|right)-0.95\t_{2}le0$

Теперь “окошки”, чтобы у букв появились вертикальные элементы

$maxleft(left|1.2left|x_{1}right|-1.2right|,left|y_{1}-0.9right|right)-1ge0$

Теперь V-образные элементы

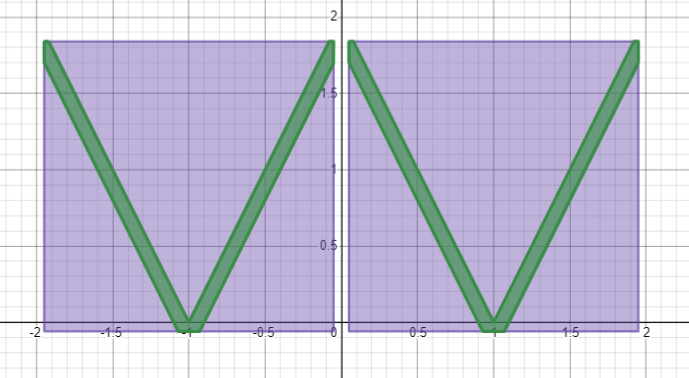
$minleft(left|2left|x_{1}right|-2right|-y_{1},-left|2left|x_{1}right|-2right|+y_{1}+0.2,-t_{2}right)ge0$

Скомбинируем в одну формулу

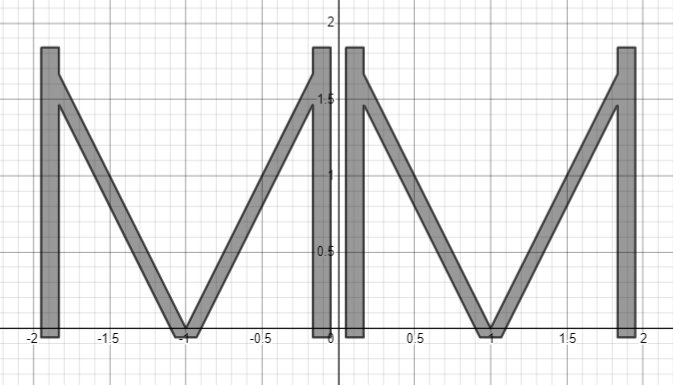
$maxleft(minleft(-t_{2},maxleft(left|1.2left|x_{1}right|-1.2right|,left|y_{1}-0.9right|right)-1right),minleft(left|2left|x_{1}right|-2right|-y_{1},-left|2left|x_{1}right|-2right|+y_{1}+0.2,-t_{2}right)right)ge0$

Две буквы “Х”

Применяем знакомые ограничители

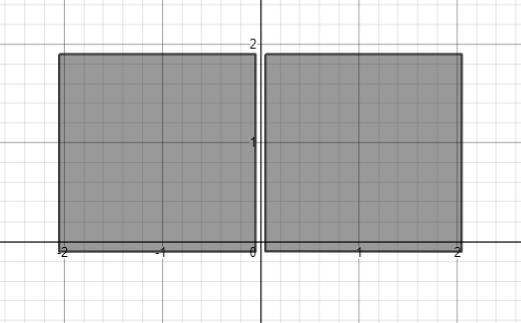
$maxleft(left|left|x_{1}right|-1.05right|,left|y_{1}-0.9right|right)-1le0$

Крестообразные элементы

$minleft(left|left|x_{1}right|-1.05right|-left|y_{1}-0.9right|, -left|left|x_{1}right|-1.05right|+left|y_{1}-0.9right|+0.15right)ge0$

Объединим

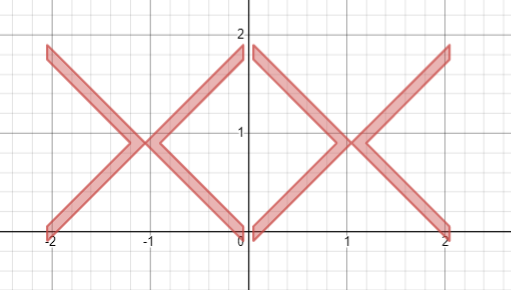
$maxleft(-minleft(left|left|x_{1}right|-1.05right|-left|y_{1}-0.9right|, -left|left|x_{1}right|-1.05right|+left|y_{1}-0.9right|+0.15right),maxleft(left|left|x_{1}right|-1.05right|,left|y_{1}-0.9right|right)-1right)le0$

Сдвинем на 4.1 вправо, теперь ХХ займут своё место

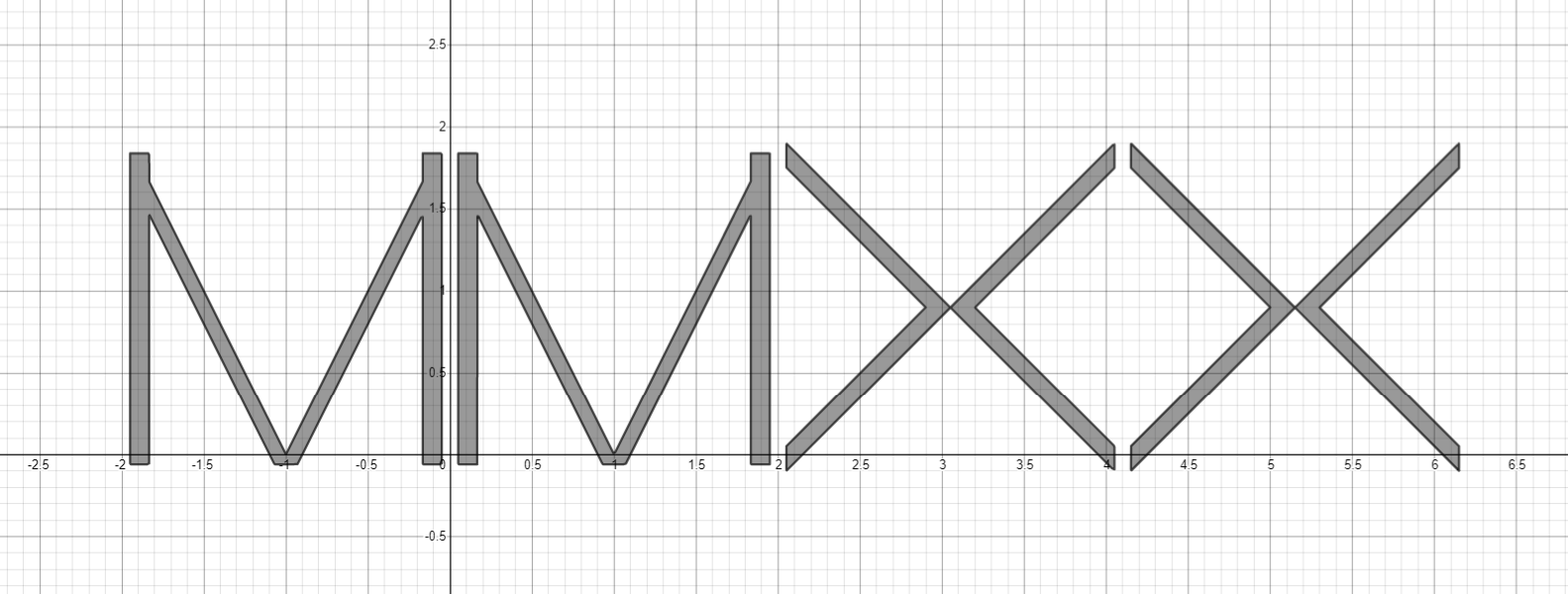
$maxleft(-minleft(left|left|x_{1}-4.1right|-1.05right|-left|y_{1}-0.9right|, -left|left|x_{1}-4.1right|-1.05right|+left|y_{1}-0.9right|+0.15right),maxleft(left|left|x_{1}-4.1right|-1.05right|,left|y_{1}-0.9right|right)-1right)le0$

Одна буква “I”

Тривиально, сразу же поставим “I” на её место

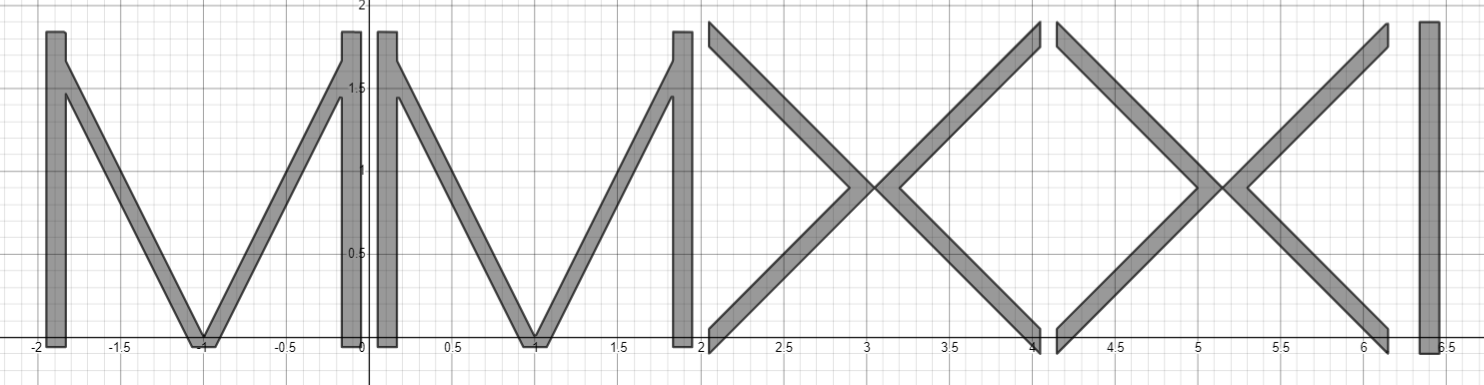
$maxleft(left|x_{1}-6.4right|-0.06,left|y_{1}-0.9right|-01right)le0$

Все формулы для букв

t_{2}=maxleft(left|left|x_{1}right|-1right|,left|y_{1}-0.89right|right)-0.95

maxleft(minleft(-t_{2},maxleft(left|1.2left|x_{1}right|-1.2right|,left|y_{1}-0.9right|right)-1right),minleft(left|2left|x_{1}right|-2right|-y_{1},-left|2left|x_{1}right|-2right|+y_{1}+0.2,-t_{2}right)right)ge0

maxleft(-minleft(left|left|x_{1}-4.1right|-1.05right|-left|y_{1}-0.9right|, -left|left|x_{1}-4.1right|-1.05right|+left|y_{1}-0.9right|+0.15right),maxleft(left|left|x_{1}-4.1right|-1.05right|,left|y_{1}-0.9right|right)-1right)le0

Сдвинем локальную систему координат

$x_{1}=left(x -8right)cdot1.3\y_{1}=left(y-9.3right)cdot1.3$

Краткие замечания по работе

Первое, на что хочется обратить внимание – то, что для рисунка применялись функции, неограниченные искусственно, как например sin(x), x∈(-5, 5). Все ограничения создаются естественным путём на базе арифметических операций с функциями.

Минимум и максимум также можно выразить с помощью простейших операций:

$min=frac{f+g}{2}-left|frac{f-g}{2}right|\max=frac{f+g}{2}+left|frac{f-g}{2}right|$

Поэтому использование функций min и max в формулах фигур легально в данной задаче.

Let’s block ads! (Why?)

Базовые функции

Трапеция

Альтернативный эллипс

Эллипс по двум точкам

Прямоугольник

Снеговик

Тело – три эллипса

Ведро на голову!

Шаг первый – трапеция

Шаг второй – доработаем форму, поднимем ведро

Шаг третий – ограничение снизу

Шаг пятый – наденем ведро на голову

Руки – эллипсы

Тело снеговика по элементам

Результат тела снеговика

Лицо

Глаза – 2 круга

Рот – два эллипса

Все функции снеговика для вставки в desmos

Сугробы

Суммируем

Результат

Все функции сугробов

Снежинки

Много снежинок

Результат

Корректировка снежинок

Комбинируем

Все формулы снежинок

Подарки под ёлку

Бантики к подаркам

Модуль

Гипербола

Круг

Эллипс

Внезапный ход: множим эллипс на модуль

Комбинируем все элементы

Все формулы для бантиков

Цифры

Две буквы “М”

Скомбинируем в одну формулу

Две буквы “Х”

Объединим

Одна буква “I”

Все формулы для букв

Сдвинем локальную систему координат

Краткие замечания по работе

Опубликовано

Добавить комментарий Отменить ответ