Практическое применение алгоритма для представления Цекендорфа

Как то в прошлом

Я написал статью о рекурсивном алгоритме Цекендорфа : пост

def le_fib(limit, fib)
  theoretical = fib[fib.count - 1] + fib[fib.count - 2]
  return fib.last if theoretical > limit

  fib << theoretical
  le_fib(limit, fib)
end

def main(target,result)
  temporary = le_fib(target, [1,1])
  result << temporary
  return result if target - temporary <= 0

  main(target - temporary, result)
end
pp main(gets.to_i,[])

Хотя по правде говоря в комментах предложили более изящное решение :

n, F = 100, [1, 2]
while F[-1] < n do
  F << F[-2] + F[-1]
end
F.reverse.each do |f|
  if f <= n
    n -= f
    print f
    print '+' if n > 0
  end
end

На практике я буду применять именно второй алгоритм так как он мение перегружен лишними действиями.

Постановка задачи куда мы будем “впихивать этот алгоритм”

Есть некий набор продуктов, условно говоря :

[ Курица, томаты, лаваш, грибы ].

Эти продукты имеют ценность, как себестоимость так и ценность для конечного пользователя.
К примеру градацию можно произвести такую

[ курица > томаты > грибы > лаваш ] .

Задача состоит в том что бы генерировать такой набор продуктов, который имел бы по крайней мере 1 “Low cost“, и 1 “High cost” продукт.

Вот тут то я хочу присбособить этот алгоритм (Цекендорфа).

Главная идея в том что бы создать хэш (структура данных в Ruby) где ключ это число фиббоначи, а значение собственно имя продукта.

Задача есть, теперь перейдем к решению.

Для начала анализируем сам алгоритм

Запустим его в цикле от x до y и посчитаем количество вхождений каждого числа.

1. 

   

2. Как видим на малых Y вероятность того что число будет использовано в последовательности – равномерно распределенно так как верхняя граница чисел Фибоначчи постоянно растёт пропорционально к текущему числу в итерации.

   Что мы с этого получили – чем больше входное число, тем выше вероятность получения одного и того же граничнего числа последовательности Фибоначчи.

   Значит нам нужен отрезок с более равномерным распределением. Уменьшаем Y

   

3. Видим пик на крайних числах 1 и 89. Что собственно отвечает постановки задачи, но при этом мы не теряем случайное равномерное выпадение “Middle cost” продуктов.

   Предлагаю остановится на 3 варианте где x = 1 и y = 143.

Реализация

Программы куда будем прописывать алгоритм Цекендорфа, выглядит так :

• Модуль-перечень продуктов (для возможной тематичности)

• Collector, который загружает перечень продуктов и составляет Hash (где ключ -> число Фибоначчи, значение -> название продукта)

Такую струтуру я использую для возможной тематичности продуктов, достаточно просто создать новый перечень продуктов и передать в autoloader название новой тематики, что бы времено ввести новые продукты в оборот.

К слову говоря, всё это я делаю для Telegram бота , который создан по гайду описаном в другом посте.

Итак, написав небольшой парсер, на выходе получаем такой результат

@fib = [1,2,3,5,8,13,21,34,55,89]
    def collect_the_items
      food_hash = Hash.new
      (0..9).each do |iterator|
        food_hash[@fib[iterator]] = FOOD.first[iterator]
      end
      puts food_hash.map{|key,value| "#{key} - #{value}"}
    end

Следующим шагом, слегка изменим алгоритм представления Цекендорфа :

def get_sequence(limit)  
  result = []  n, fib = limit, [1, 2]  
  while fib[-1] < n do
    fib << fib[-2] + fib[-1]  end
  fib.reverse.each do |f|    if f <= n
      n -= f
      result << f
    end
  end
  result
end

Я собираюсь использовать готовую последовательность и пройдя по ней – просто вывести все продукты по ключам.

def generate_food
          food_array = Collector.collect_the_items
          food = []
          rarity = rand(1..143)
          get_sequence(rarity).each do |key|
            food << food_array[key]
          end
          food
end

Похоже всё готово к тесту, проведу 6 тестовых прогонов, результаты будут в виде ответа от телеграмм бота.
Немного украшу сообщение от бота. Поскольку это никак не отражается на задаче – я не буду описывать этот шаг.

Результаты теста

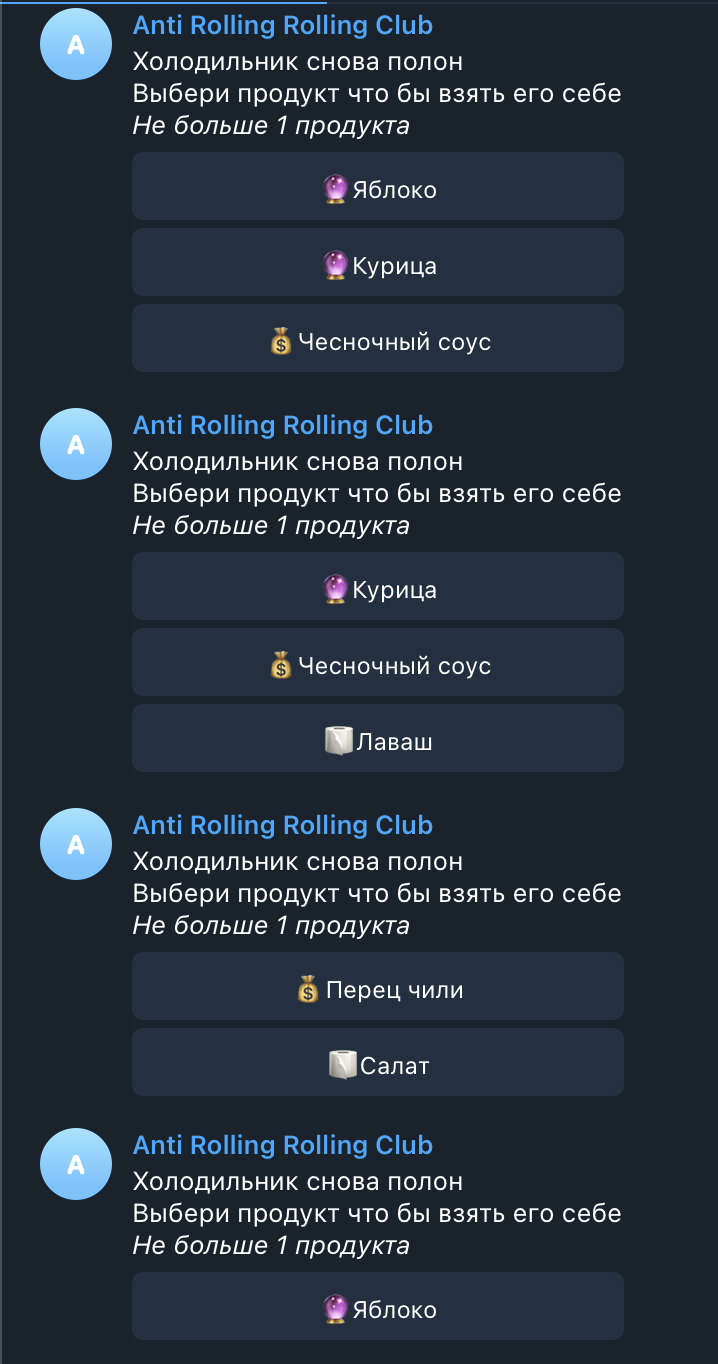
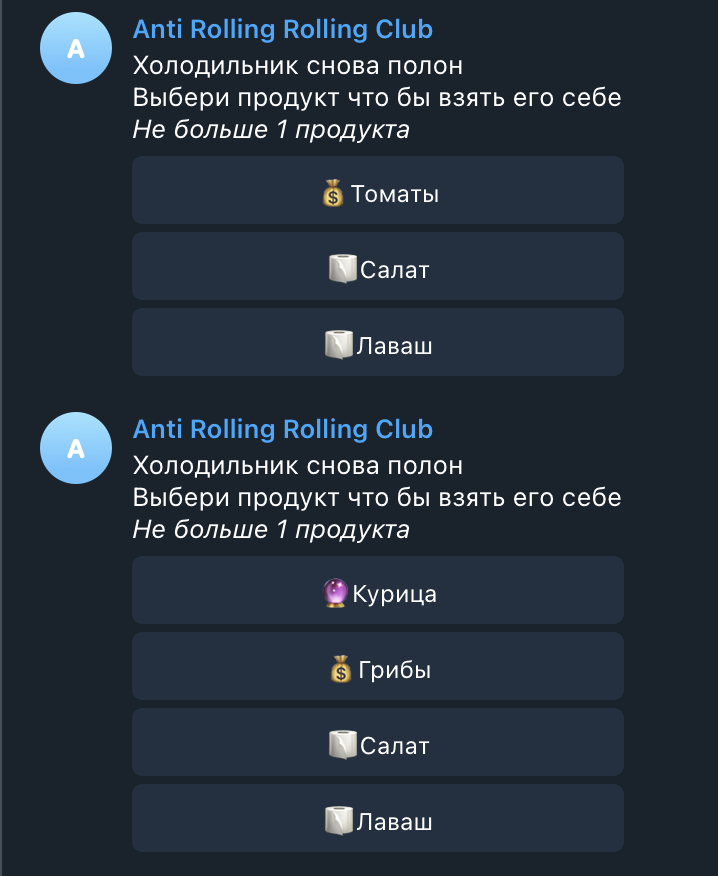
примечание :
Low cost : ?
Mid cost : ?
High cost : ?

Результат

Применения алгоритма представления Цекендорфа меня полностью удовлетворяет. Тоесть – выполняет поставленную перед ним задачу.

Один из первых комментов под статьей на которой основано это практическое приминение, как раз таки и ставил перед мной вопрос : “а действительно, где это применить можно?”. Как видим, вот для таких задач данный алгоритм вполне можно использовать.

И я не говорю о том что это единственный правильный вариант составления списка продуктов для моего бота, но он действительно вполне потян и работает.