Чистый Cython VS nvc++: жжем металлические пластины на GPU для сравнения скорости

Будем греть металлические пластины на GPU
Все знают, что Python не блещет скоростью сам по себе. На мой взгляд язык прекрасен своей читабельностью, но основная ниша его применения там, где вы большую часть времени ожидаете ввода/вывода каких-то данных. Условно, вы можете написать суперпроизводительный код на Rust или С, но 99% времени он будет просто ждать.
Тем не менее, Python прекрасен еще и как высокоуровневый синтаксический клей. В этом случае, его неторопливая интерпретируемая часть вызывает быстродействующий код, написанный на компилируемых языках программирования. Обычно для этого используются такие традиционные библиотеки как NumPy.
Но мы пойдем чуть дальше попробуем распараллелить вычисления на CUDA и задействуем странный, но работающий гибрид C++, stdpar и компилятора nvc++ от Nvidia. Ну и заодно попробуем оценить быстродействие. Возьмем две задачи: сортировку чисел и метод Якоби, которым будем рассчитывать нагрев металлической пластины.
Вызываем C++ из Python
Наш код сортировки будет иметь следующий вид:
# distutils: language=c++
from libcpp.algorithm cimport sort
def cppsort(int[:] x):
sort(&x[0], &x[-1] + 1)
В первой строчке мы явно указываем, что Cython должен использовать C++, а не дефолтный C. Во второй мы импортируем функцию сортировки из C++, а дальше следует сама логика. Помещаем код в файл cppsort.pyx. Обратите внимание, что расширение отличается от привычного py, так как мы будем его компилировать или выполнять cythonize в терминологии Cython.
Компиляцию можно выполнить вручную или включить в setup.py, где мы полноценно описываем подготовку нашего окружения.
В setup.py это выглядит примерно так:
from setuptools import setup
from Cython.Build import cythonize
setup(
ext_modules = cythonize("cppsort.pyx")
)
Но мы можем и просто выполнить это в командной строке:
cythonize -i cppsort.pyx
Под капотом произойдет примерно следующее:

- Cython транслирует python код в C++ и сгенерирует валидный cppsort.cpp.
- C++ компилятор (в данном случае g++) компилирует C++ код в Python extension module
- Python extension module импортируется в код как обычный питоновский модуль.
После компиляции можем импортировать и сразу протестировать сортировку:
from cppsort import cppsort
import numpy as np
x = np.array([4, 3, 2, 1], dtype="int32")
print(x)
cppsort(x)
print(x)
Массив [4, 3, 2, 1] успешно отсортируется в [1, 2, 3, 4] с помощью C++ std::sort.
А давайте на GPU?
Стандартные библиотечные алгоритмы C++ могут вызываться с указанием аргумента parallel execution policy. Этот аргумент говорит компилятору о том, что вы хотите раскидать алгоритм на параллельные процессы.
При этом C++ имеет несколько вариантов этой политики:
- std::execution::seq: Последовательное выполнение. Параллельность запрещена.
- std::execution::unseq: Векторизированное выполнение в рамках вызвавшего потока.
- std::execution::par: Параллельное выполнение в одном и более потоках.
- std::execution::par_unseq: Параллельное выполнение в одном и более потоках. Каждый поток будет по возможности векторизирован.
При этом вы сами должны следить за race condition и deadlock. Стандартный компилятор g++ постарается распределить вычисления на ядра CPU. Но мы можем взять проприетарный компилятор от Nvidia — nvc++ и скормить ему опцию “-stdpar”. stdpar — это C++ Standard Parallelism от Nvidia с выполнением параллельного кода на GPU.
Перепишем код, с учетом необходимости создавать локальную копию массива, так как GPU не сможет получить доступ к массиву, расположенному в рамках NumPy.
from libcpp.algorithm cimport sort, copy_n
from libcpp.vector cimport vector
from libcpp.execution cimport par
def cppsort(int[:] x):
cdef vector[int] temp
temp.resize(len(x))
copy_n(&x[0], len(x), temp.begin())
sort(par, temp.begin(), temp.end())
copy_n(temp.begin(), len(x), &x[0])

Теперь это нужно снова скомпилировать, но уже с использованием nvc++. В этот раз напишем нормальный setup.py и вызовем его:
CC=nvc++ python setup.py build_ext --inplace
Импортируем в код и пробуем вызвать:
x = np.array([4, 3, 2, 1], dtype="int32")
cppsort(x) # этот кусок выполняется на GPU
Производительность
Традиционно GPU хороши там, где есть много однотипных легковесных вычислений. Тяжелые задачи одиночные задачи GPU не подойдут. Более того, стоит учитывать объем ваших данных. Если у вас немного данных, то вы получите большой оверхед на процесс распараллеливания, ввод/вывод на между CPU и GPU. В итоге, такой код скорее всего наиболее эффективно будет выполняться на чистом CPU, иногда даже в пределах одного ядра, если данных совсем немного. Но на больших массивах GPU однозначно будет впереди.
Вот тут есть отличное сравнение сортировки. За единицу брали скорость NumPy, а затем считали кратность прироста скорости в каждом методе относительно него.
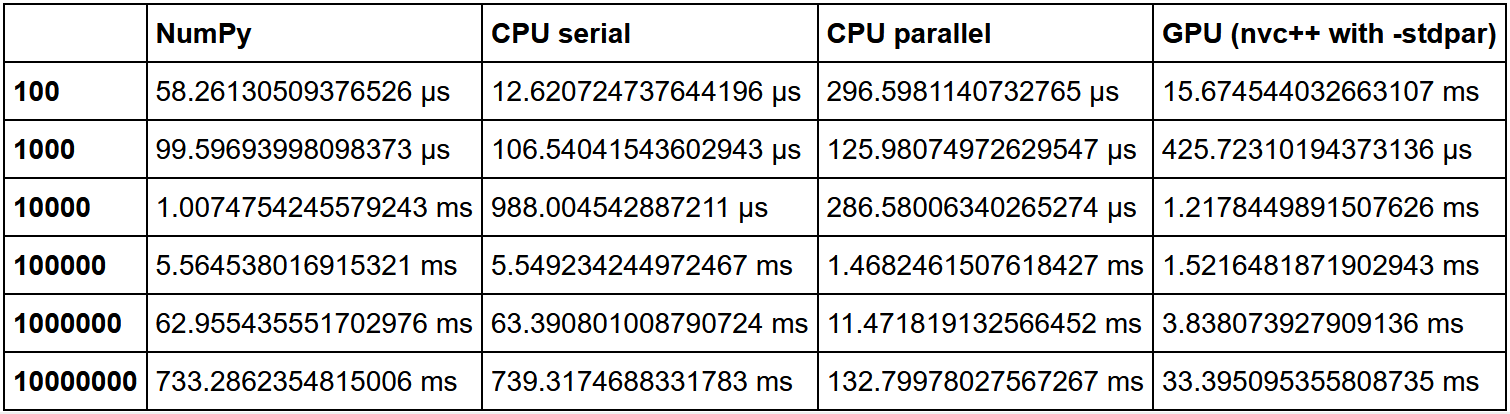
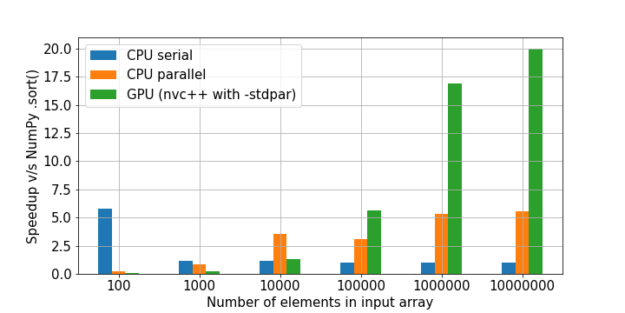
Как мы видим, гипотеза о том, что выигрыш в использовании GPU на большом количестве данных растет, подтверждается.
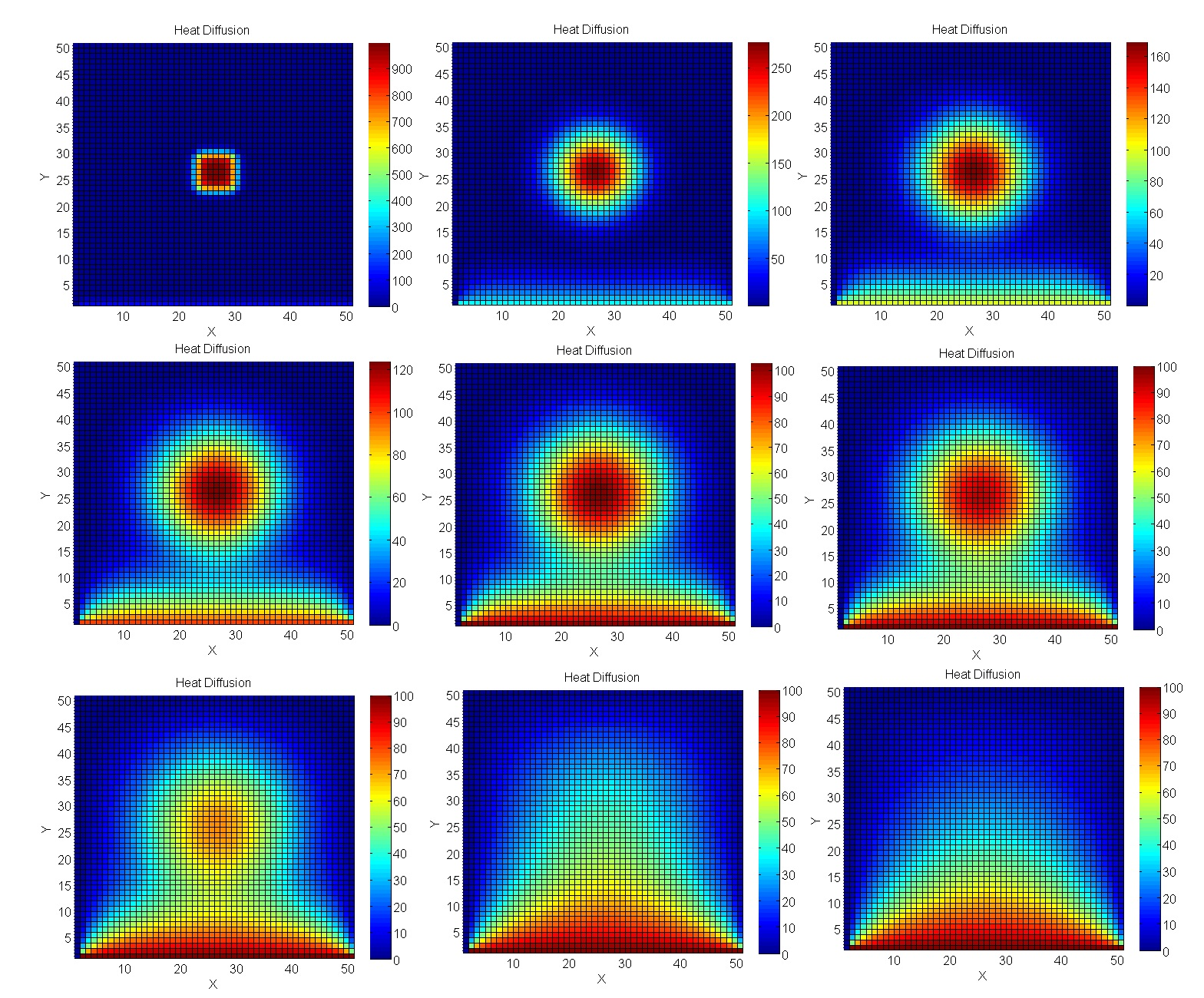
Вычисляем нагрев пластины
Возьмем задачу более приближенную к реальному инженерному моделированию — вычислениям по методу Якоби. В частности, они отлично подходят для вычисления температурных процессов в 2D-пространстве.

"""
simulates heat equation on rectangle returning a heat map at a number of times
boundary and initial conditions are 0, source represents burner on a stove
This program is based on the script FEniCS tutorial demo program: Diffusion of a Gaussian hill.
u'= Laplace(u) + f in a square domain
u = u_D = 0 on the boundary
u = u_0 = 0 at t = 0
u_D = f = stove burner flame
This program succesfully runs in the fenics docker image, see the book Solving PDEs in Python.
to animate: convert -delay 4 -loop 100 heatequation10*.png heatstovelinn.gif
to crop:convert heatstovelinn.gif -coalesce -repage 0x0 -crop 810x810+95+15 +repage heatstovelin.gif
"""
from fenics import *
import time
import matplotlib.pyplot as plt
from matplotlib import cm
# Create mesh and define function space
nx = ny = 100
mesh = RectangleMesh(Point(-2, -2), Point(2, 2), nx, ny)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary, source, initial
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, Constant(0), boundary)
u_0 = interpolate(Constant(0), V)
f = Expression('exp(-sqrt(pow((a*pow(x[0], 2) + a*pow(x[1], 2)-a*1),2)))', degree=2, a=5) #steep guassian centred on the unit sphere
final_time = 0.035
num_pics = 72
for i in range(num_pics):
T = final_time*(i+1.0)/(num_pics+1) #solve time even space
#T = final_time*1.1**(i-num_pics+1) #solve time log space
num_steps = 30
dt = T / num_steps # time step size
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
F = u*v*dx + dt*dot(grad(u), grad(v))*dx - (u_0 + dt*f)*v*dx
a, L = lhs(F), rhs(F)
# Time-stepping
u = Function(V)
t = 0
for n in range(num_steps):
t += dt #step
solve(a == L, u, bc) #solve
u_0.assign(u) #update
#plot solution
plot(u,cmap=cm.hot,vmin=0,vmax=0.07)
plt.axis('off')
plt.savefig('heatequation10%s.png'%(i+10),figsize=(8, 8), dpi=220,bbox_inches='tight', pad_inches=0,transparent=True)
Напишем аналогичный солвер на Cython для последующей компиляции по CUDA:
# distutils: language=c++
# cython: cdivision=True
from libcpp.algorithm cimport swap
from libcpp.vector cimport vector
from libcpp cimport bool, float
from libc.math cimport fabs
from algorithm cimport for_each, any_of, copy
from execution cimport par, seq
cdef cppclass avg:
float *T1
float *T2
int M, N
avg(float* T1, float *T2, int M, int N):
this.T1, this.T2, this.M, this.N = T1, T2, M, N
inline void call "operator()"(int i):
if (i % this.N != 0 and i % this.N != this.N-1):
this.T2[i] = (
this.T1[i-this.N] + this.T1[i+this.N] + this.T1[i-1] + this.T1[i+1]) / 4.0
cdef cppclass converged:
float *T1
float *T2
float max_diff
converged(float* T1, float *T2, float max_diff):
this.T1, this.T2, this.max_diff = T1, T2, max_diff
inline bool call "operator()"(int i):
return fabs(this.T2[i] - this.T1[i]) > this.max_diff
def jacobi_solver(float[:, :] data, float max_diff, int max_iter=10_000):
M, N = data.shape[0], data.shape[1]
cdef vector[float] local
cdef vector[float] temp
local.resize(M*N)
temp.resize(M*N)
cdef vector[int] indices = range(N+1, (M-1)*N-1)
copy(seq, &data[0, 0], &data[-1, -1], local.begin())
copy(par, local.begin(), local.end(), temp.begin())
cdef int iterations = 0
cdef float* T1 = local.data()
cdef float* T2 = temp.data()
keep_going = True
while keep_going and iterations < max_iter:
iterations += 1
for_each(par, indices.begin(), indices.end(), avg(T1, T2, M, N))
keep_going = any_of(par, indices.begin(), indices.end(), converged(T1, T2, max_diff))
swap(T1, T2)
if (T2 == local.data()):
copy(seq, local.begin(), local.end(), &data[0, 0])
else:
copy(seq, temp.begin(), temp.end(), &data[0, 0])
return iterations

В итоге отрыв GPU получается еще более существенным.
Минусы
- Написание такого кода несколько сложнее, чем чистого варианта на Python и требует понимания принципов работы параллельных вычислений на GPU.
- Требуется копирование данных в отдельный массив для передачи на GPU, куда видеокарта не имеет доступа. Это может быть проблемой при работе с очень большими массивами.
