Что за зверь — афинные преобразования?
Скорее всего, каждый из Вас хоть раз в жизни слышал термин «афинные преобразования». Действительно, все постоянно о них говорят: «инвариантность к афинным преобразованиям», «аугментация с помощью афинных преобразований», «афинные преобразования в компьютерной графике» и так далее. Однако, далеко не все могут сходу ответить на простой вопрос: «А расскажите, что такое афинные преобразования простыми словами».
Вы сможете? В любом случае, давайте немного обсудим этот вопрос.
Что такое афинное преобразование?
Начнем с классики – определение из Википедии.
Аффинное преобразование (от лат. affinis «соприкасающийся, близкий, смежный») — отображение плоскости или пространства в себя, при котором параллельные прямые переходят в параллельные прямые, пересекающиеся — в пересекающиеся, скрещивающиеся — в скрещивающиеся.
Внесем немного ясности.
Во-первых, что значит «отображение в себя»? Это значит, что если мы находились в пространстве , то после образования мы должны остаться в нем же. Например: если мы применили какое-то преобразование к прямоугольнику и получили параллелепипед, то мы вышли из
в
. А вот если из прямоугольника у нас получился другой прямоугольник, то все хорошо, мы отобразили исходное пространство в себя. Формально это описывается так: «преобразование
отображает пространство
в
». Если записать с помощью формул:
.
Во-вторых, что такое «скрещивающиеся прямые»? Конечно, все это проходили в школе, но на всякий случай напомним. Прямые называются скрещивающимися, если они не лежат в одной плоскости. Вот если бы они лежали в одной плоскости и пересекались, они назывались бы пересекающимися. А если в разных плоскостях, то скрещивающимися. Пример – на рисунке.
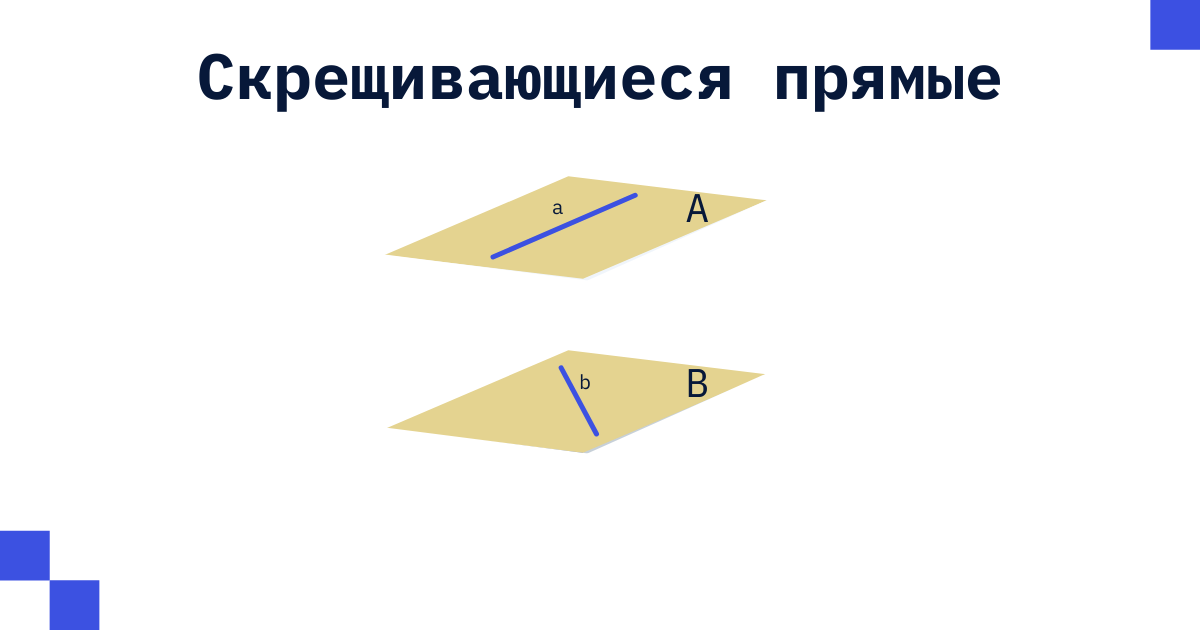
В целом, это определение уже нам что-то говорит и мы начинаем потихоньку рисовать для себя картинку. Как минимум, мы должны остаться в той же плоскости: значит мы представляем себе декартову систему координат. Здесь речь идет о нескольких прямых, так что давайте представим 2 параллельных линии. Из определения мы понимаем, что после преобразования эти линии должны остаться параллельными. Ну что ж, тогда просто сдвигаем их куда-нибудь из исходного местоположения, да и все.
По сути, мы с Вами только что описали один из видов афинных преобразований – сдвиг.
Но давайте пойдем чуть дальше и дадим еще одно определение (не нами придуманное).
Преобразование плоскости называется аффинным, если оно непрерывно, взаимно однозначно и образом любой прямой является прямая.
Звучит это, пожалуй, чуть сложней и путанней, но дает нам больше конкретной информации, чем предыдущее определение.
Преобразование называется непрерывным, если «близкие точки переходят в близкие». Т.е. иначе – если у нас есть две точки и они находятся рядом, то после преобразования они все равно будут находиться где-то поблизости друг от друга.
Далее – преобразование взаимооднозначно, если разные точки переводятся в разные точки и в каждую точку переводится какая-то точка. Например: если мы отобразили отрезок и он слипся в точку – это не взаимооднозначное преобразование. Из отрезка мы должны получить ровно такой же отрезок, тогда будет взаимооднозначно (если это сработает для всех отрезков, конечно).
Итак, с определениями мы разобрались. Давайте теперь запишем в общем виде, а как выглядит преобразование координат в формульном виде.
Пусть у нас есть исходная система координат. Точка в этой системе характеризуется двумя числами – и
. Совершить переход к новым координатам
и
мы можем с помощью следующей системы:
При этом, числа должны образовывать невырожденную матрицу:
На всякий случай: матрица называется невырожденной, если ее определитель не равен нулю, т.е.
Можно записать и в более общем в виде.
Афинное преобразование – преобразование вида
, где
– обратимая матрица, а
. В данном случае
, само собой,
-мерный вектор.
Примеры афинных преобразований
Мы с Вами достаточно подробно разобрали, что такое афинное преобразование и как его можно описать с помощью формул. Давайте теперь рассмотрим популярные примеры.
Приходят ли Вам в голову какие-нибудь претенденты на роль? Позвольте мы внесем свои предложения.
Поворот
Пусть .
Значит, матрица примет вид:
И новые координаты будут выглядеть так:
Ничего не напоминает? Если Вы еще не узнали, то встречайте – это просто повернутая система координат на угол . Т.е. мы применили афинное преобразование и наша система координат повернулась. Пример этого Вы можете видеть на графике.

Растяжение-сжатие
Теперь мы предлагаем сконструировать матрицунесколько иначе:
Новые координаты тогда принимают вид:
В целом, тут даже уже из вида системы уравнений понятно, что мы просто растягиваем наши оси, если коэффициент меньше 1 и сжимаем, если больше 1. Пример на рисунке.
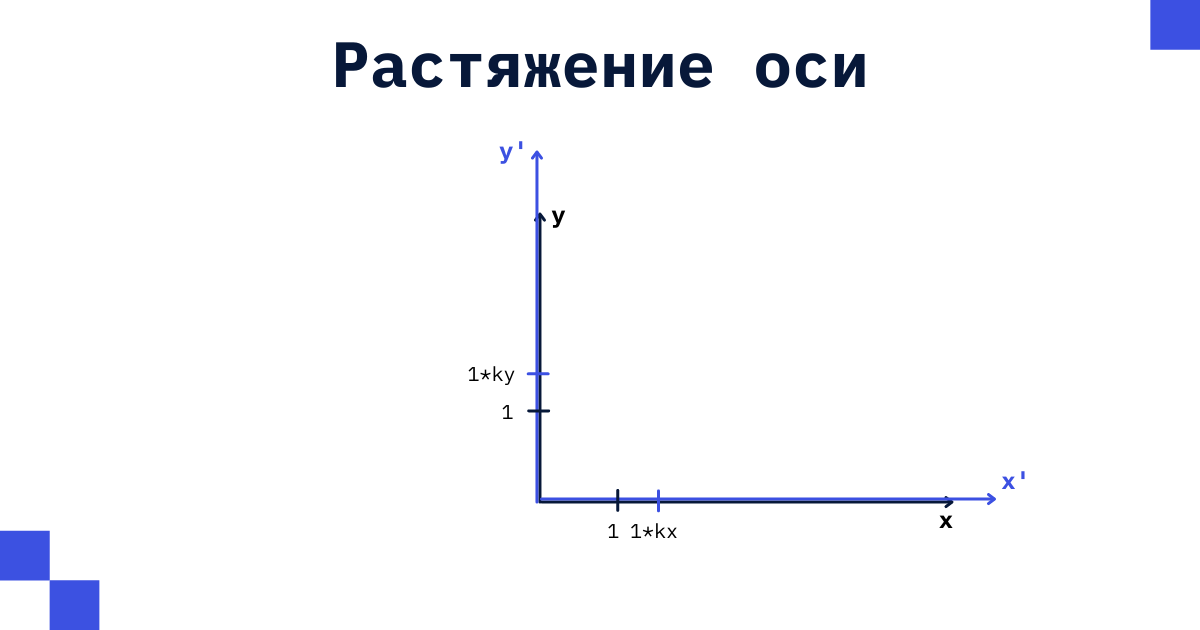
Кстати говоря, а попробуйте поставить вместо число -1, а вместо
просто 1. Что получится? Правильно, мы просто отразим нашу систему координат относительно оси
.
Сдвиг
Ну и давайте напоследок еще один пример.
Пусть теперь матрица никак не меняет исходные координаты (т.е.
). А вот
пусть равняется
, а
.
Таким образом, наша система принимает вид:
Если отразить это на графике, то мы просто сдвинули начало координат в точку . Вот, собственно, и вся премудрость.

Эпилог
Эта короткая статья позволит Вам чуть сильней прочувствовать «внутренности» афинных преобразований (мы надеемся на это). После прочтения попробуйте все-таки ответить на вопрос, который мы ставили в самом начале – «А расскажите, что такое афинные преобразования простыми словами». Теперь сможете?
P.S. Кстати говоря, было бы неплохо не верить нам на слово и проверить самим – а матрицы , которые мы использовали – точно невырожденные? Может мы вообще что-то противозаконное сделали?…