О реализации точного представления чисел или «где хранить деньги?»

Введение
«Где хранить деньги?» это шутливое название поста, периодически появляющегося на компьютерных форумах. Имеется в виду вопрос: в переменных какого типа следует хранить результаты вычислений финансово-экономических расчетов. Обычно такой вопрос возникает у программистов, впервые сталкивающихся с подобными расчетами. Интуитивно они понимают, что здесь округления нежелательны или недопустимы. Интересно, что при этом часто вспоминают легенды о хитрых программистах, сумевших разницу между точным и округленным значением финансовых расчетов перечислять на свой собственный счет. Правда, эти истории названы сказками еще в книге [1], написанной 50 лет назад, причем даже там речь шла лишь о ревизиях банковских систем, основаниями для которых (т.е. для ревизий) могли бы служить подобные истории.
Компьютеры применяются для экономических расчетов уже более 60 лет. Приемы и инструменты таких расчетов хорошо развиты и изучены. Тем не менее, поскольку все-таки возникают вопросы, подобные вынесенному в заголовок, представляется полезным для лучшего понимания проблем экономических расчетов привести как пример одну из самых простых и проверенных временем реализаций в трансляторе аппарата «точных» вычислений и его особенностей. Под «точными» далее будут подразумеваться вычисления без округлений и с исходными данными, представленными в виде десятичных дробей. Разумеется, не все данные можно точно представить в десятичном виде, поэтому понятие «точный» здесь имеет некоторые ограничения, однако для экономических расчетов в большинстве случаев эти ограничения несущественны.
Пример необходимости точных вычислений
Рассмотрим простейший пример: рассчитать выплату 13% с суммы 1 рубль 30 копеек. Это значение легко сосчитать на бумаге «столбиком» и притом точно: 16.9 копейки. Но если запрограммировать этот же расчет с использованием данных типа «double», то получится ответ вроде 1.68999999999999E-001 рубля, поскольку значение 0.169 точно представить в формате IEEE-754 нельзя. Вот тут и начинаются сомнения: не приведет ли ряд подобных вычислений к накоплению погрешности? Определение итоговой погрешности для нетривиальных расчетов само является нетривиальной математической задачей и лучший способ ее решения – не допускать погрешностей вообще. Но как это сделать? И какой тип данных должен быть, если тип «целый» не годится, а тип «float» обязательно даст погрешность?
Виды представления чисел
Может показаться, что автор ломится в открытую дверь. Есть же в языках типы для работы с «деньгами», например, тип DECIMAL в языке C#. Как следует из описания языка [2], «Тип значения Decimal подходит для финансовых вычислений, требующих большого количества значимых целых и дробных цифр и отсутствия ошибок округления. Избежать округления с помощью типа Decimal нельзя. Однако он позволяет минимизировать связанные с ним ошибки». Странно, требуется избежать ошибок округления и одновременно утверждается, что этого сделать нельзя.
Одной из причин затруднений в таких случаях является, на мой взгляд, не совсем четкая классификация представления чисел. Многие привыкли делить числа только на целые и действительные, хотя правильнее было бы вначале разделить их на точные и приближенные. При этом целые – это подмножество точных, а не все множество. В приведенном примере расчета «на бумаге» хотя и получились копейки с долями, т.е. нецелое значение, никакой потери точности не произошло. Тип DECIMAL в языке C# корректнее было бы назвать «модифицированным FLOAT», поскольку он содержит те же знак, мантиссу и порядок. И значения этого типа все же приближенные, хотя и с очень большим числом значащих цифр.
Аппаратная поддержка точных вычислений
А ведь в процессорах архитектуры IA-32 имеется набор специальных команд так называемой десятичной и двоично-десятичной арифметики. Они предназначены как раз для проведения точных вычислений. Удивительно, но в 64-разрядном режиме эти команды становятся недоступными, можно предположить, что в фирме Intel разработчики заранее «расчищают» кодовое пространство для новых команд. Но в 32-разрядном режиме такие команды доступны, упрощая вычисления со сколь угодно большой точностью и без округлений. Для проверки автор задавал вопросы коллегам по поводу назначения двоично-десятичной арифметики и убедился, что многие имеют о ней нечеткие представления, например, отвечая, что она нужна только для того, чтобы не переводить число из текста в двоичное и обратно. Такой ответ тоже допустим, поскольку числа действительно представлены не в «обычном» виде. Но все-таки следует еще раз подчеркнуть, что главное назначение нестандартной арифметики – упростить организацию вычислений без потери точности.
Программная поддержка точных вычислений
Механизм вычислений без округлений был встроен, например, в язык PL/1. Этот язык изначально разрабатывался для применения и в области экономических расчетов, для чего он получил «наследство» от языка экономических задач Кобола. Можно даже предположить, что команды двоично-десятичной арифметики были вставлены в архитектуру IA-32 (точнее, еще в IA-16 в 1978 году) именно для поддержки в языках высокого уровня типа PL/1 аппарата точных вычислений. Поскольку автор сопровождает и использует транслятор языка PL/1 [3], дальнейшее изложение будет относиться к конкретной реализации. Сама реализация довольна проста и объем команд транслятора, обеспечивающих генерацию точных вычислений, не превышает 3-4% от размера транслятора.
Представление чисел FIXED DECIMAL
Граница между представлениями чисел в PL/1 проведена корректно: все числа точного представления имеют тип FIXED, а приближенного представления – FLOAT. К сожалению, сами названия «FIXED/FLOAT» (вместо «ТОЧНОЕ/ПРИБЛИЖЕННОЕ») не вносят ясности и интуитивно непонятны. Как, кстати, и распространенное в языках, но совершенно неинформативное название «double».
В операторах описания на PL/1 точное представление чисел имеет атрибуты FIXED DECIMAL, после которых указывается общий размер числа и размер дробной части числа, например, FIXED DECIMAL(15,0)или FIXED DECIMAL(12,4) т.е. так можно точно представлять и целые и нецелые значения. Значения можно также представлять и как FIXED BINARY, но далее будет рассматриваться только тип, который может иметь десятичную дробную часть.
В рассматриваемом трансляторе этот тип реализован в двоично-десятичном упакованном коде BCD (Binary Coded Decimal). Каждая цифра BCD записывается в половину байта. При этом старшая значащая пара цифр BCD размещается по старшему адресу. Самая старшая позиция BCD резервируется для знака, который для положительных чисел – ноль, для отрицательных – девять. Число байт для FIXED DECIMAL определяется заданной «точностью» p (допустимой в стандарте языка от 1 до 15) и равно FLOOR((p+2)/2).
Например, число 12345 с точностью 5, для которого PL/1 выделит FLOOR((5+2)/2)=3 байта памяти, будет записано в байтах как 45 23 01. Максимально допустимое значение, которое можно записать в таком виде 999 999 999 999 999. Например, чтобы представить точно значение государственного долга США, который,например, на начало 2013 года составлял около $16,400,000,000,000, потребуется переменная типа FIXED DECIMAL(14,0). Правда, если долг вырастет еще раз в 60, представить его точно в формате стандарта PL/1 будет уже нельзя.
Отрицательное число записывается в дополнительном до 9 коде, который получается вычитанием каждой цифры из 9 и прибавлением к числу единицы. Например, число -2 имеет код (9-2)+1=8 и с точностью 1 будет записано как байт 98, а с точностью 5 будет выглядеть в байтах как 98 99 99.
Может показаться странным, что в этом представлении нет указания положения десятичной точки. Но ведь и в логарифмической линейке не было указателя точки – приходилось держать ее позицию в уме. В данном случае за положением десятичной точки следит транслятор и явно указывает ее как параметр при вызове подпрограмм преобразований, ввода-вывода и т.п. А при генерации самих вычислений положение точки рассчитывается транслятором так, чтобы не терялась точность, и тоже «держится в уме» пока ее не потребуется использовать. Если вернуться к примеру, при генерации умножения транслятор назначит константе 1.3 атрибуты FIXED DECIMAL(2,1), константе 0.13 – атрибуты FIXED DECIMAL(3,2), а результату (значению 0.169) атрибуты FIXED DECIMAL(6,3), совсем как при умножении «столбиком», когда «ширина» результата складывается из размеров множителей. Правда в данном случае «ширина» должна была бы быть 5, а не 6, но по особенности PL/1 он считает длину результата при точном умножении как p1+p2+1, поскольку стандарт учитывает даже случай умножения комплексных чисел по формуле (a1a2-b1b2)+(a1b2+b1a2)i, где становится возможен еще один перенос разряда.
Системные вызовы точных вычислений
Поскольку точные вычисления не могут быть реализованы за одну-две команды, транслятор генерирует множество вызовов системных подпрограмм, обеспечивающих все необходимые действия: арифметику, функции FLOOR/CEIL/TRUNC, сравнение и т.п. Операнды типа FIXED DECIMAL передаются через стек и туда же возвращается результат операции. При этом операнды всегда расширяются до максимальной длины 8 байт и дописываются или нулями или байтами 99 (для отрицательных).
Ниже приведен фрагмент исходного текста системной библиотеки, обеспечивающий функции вычитания и сложения. Для краткости, текст остальных функций в данной статье не приводится.
;══════════════════ ВЫЧИТАНИЕ DECIMAL В СТЕКЕ ═════════════════
PUBLIC ?DSUOP: ;ГЕНЕРИРУЕТСЯ ВЫЗОВ ИЗ PL/1
LEA ESI,[ESP]+4 ;НАЧАЛО 1 DECIMAL (УЧЛИ RET)
MOV ECX,8 ;МАКСИМАЛЬНАЯ ДЛИНА DECIMAL
CLC ;СБРОС ПЕРЕНОСА
LEA EDI,[ESI+ECX] ;НАЧАЛО 2 DECIMAL
;---- ЦИКЛ ВЫЧИТАНИЯ ----
M2187:MOV AL,[EDI]
SBB AL,[ESI] ;ВЫЧИТАНИЕ С КОРРЕКЦИЕЙ
DAS
STOSB ;ЗАПИСЬ РЕЗУЛЬТАТА
INC ESI
LOOP M2187
POP ECX ;АДРЕС ВОЗВРАТА
MOV ESP,ESI ;ОЧИСТКА СТЕКА
JMP ECX
;══════════════════ СЛОЖЕНИЕ DECIMAL В СТЕКЕ ══════════════════
EXTRN ?DOVER:NEAR
PUBLIC ?DADOP: ;ГЕНЕРИРУЕТСЯ ВЫЗОВ ИЗ PL/1
LEA ESI,[ESP]+4 ;НАЧАЛО 1 DECIMAL (УЧЕТ RET)
MOV ECX,8 ;МАКСИМАЛЬНАЯ ДЛИНА DECIMAL
CLC ;СБРОС ПЕРЕНОСА
LEA EDI,[ESI+ECX] ;НАЧАЛО 2 DECIMAL
;---- ЦИКЛ СЛОЖЕНИЯ ДВУХ DECIMAL В СТЕКЕ ----
M2283:LODSB
ADC AL,[EDI] ;СЛОЖЕНИЕ С КОРРЕКЦИЕЙ
DAA
STOSB ;ЗАПИСЬ ОТВЕТА
LOOP M2283
;---- ПРОВЕРКА НА ПЕРЕПОЛНЕНИЕ ----
AND AL,0F0H ;ВЫДЕЛИЛИ ПОСЛЕДНЮЮ ЦИФРУ
JZ @
CMP AL,90H ;ОТРИЦАТЕЛЬНЫЙ НЕ ПЕРЕПОЛНИЛСЯ ?
JNZ ?DOVER ;OVERFLOW ДЛЯ DECIMAL
;---- ВЫХОД С ОЧИСТКОЙ СТЕКА ----
@: POP ECX ;АДРЕС ВОЗВРАТА
MOV ESP,ESI ;ОЧИСТКА СТЕКА
JMP ECXКак следует из этого текста, для двоично-десятичной арифметики используются команды сложения и вычитания с учетом переноса (ADC/SBB) и две специфические команды коррекции результата (DAA/DAS), те самые, которые исключены в 64-разрядном режиме.
Умножение и деление требует большего числа команд, и поэтому будет выполняться медленнее, хотя в экономических расчетах объем вычислений часто невелик по сравнению, например, с объемом ввода-вывода, и сравнительно медленное выполнение арифметических операций обычно не является критичным.
Обратите внимание, что нет принципиальных ограничений на длину данных типа FIXED DECIMAL: цикл побайтной обработки пар цифр можно сделать любой длины (а, значит, и точности), хотя в соответствии со стандартом языка PL/1 под каждый операнд при вычислениях выделяется 8 байт и эта максимальная длина записана как константа. Если в трансляторе изменить предел размера типа, например с 15 до 31, а в системных подпрограммах заменить константу 8 на 16, то переменные автоматически станут получать длину до 16 байт и обрабатываться с точностью до 31 десятичного разряда теми же самыми подпрограммами. Скорость обработки при этом уменьшится.
Выполнение точных вычислений в PL/1
Вернемся к простейшему примеру точных вычислений, теперь на языке PL/1, добавив деление на ту же константу, чтобы вернуть исходное значение переменной. Вычисления проведем и для типа FIXED DECIMAL и для типа FLOAT(53) – аналога типа «double» в других языках.
test:proc main;
dcl x fixed decimal(6,3);
x=1.3;
x=x*0.13;
put skip data(x);
x=x/0.13;
put skip data(x);
dcl y float(53);
y=1.3;
y=y*0.13;
put skip data(y);
y=y/0.13;
put skip data(y);
end test;Результат вычислений представлен на рисунке.
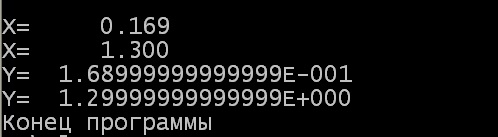
Последовательное умножение и деление на одно и то же число для типа FIXED DECIMAL вернуло точное исходное значение переменной, а для типа FLOAT – нет. Хотя, если, например, сначала разделить на три переменную типа FIXED DECIMAL, а затем умножить на три, может появиться вынужденная погрешность, обусловленная невозможностью точно представить рациональное число «одна треть» десятичной дробью.
Таким образом, аппарат точных вычислений, встроенный в язык PL/1, достаточно прост, компактен, легко реализуется в системной библиотеке и всегда готов к применению. Но иногда такие возможности играют злую шутку с программистами, ранее имевших дело только с целыми и действительными числами и даже не подозревающими о наличии в языке точных вычислений. Например, если в программе на PL/1 в числовой константе нет показателя степени E и при этом явно не указано на преобразование в тип FLOAT, то по умолчанию считается, что требуется точное представление и точные вычисления. Поэтому, например, выражение 25.0+1/3 даст исключение переполнения при выполнении, поскольку транслятор разместит рациональное число 1/3 с максимальной точностью (т.е. займет все допустимые 15 десятичных разрядов) и потом добавить еще два разряда целой части результата сложения будет уже «некуда». В то же время выражение 25.0+1Е0/3 будет вычислено приближенно и никакого переполнения не произойдет.
Все эти особенности становятся понятными и логичными, если программист ясно представляет, какой нецелый результат ему нужен в данном месте программы: точный или достаточно приближенного. Если в языке есть только целые и действительные приближенные числа, таких сложностей не возникает, но тогда возникают вопросы при необходимости провести точные вычисления с дробной частью.
Заключение
«Хранить деньги», т.е. проводить расчеты, избегая округлений, лучше всего на языках, специально разработанных для решения экономических задач типа Кобола или PL/1 или «Бухгалтерия 1С». Однако как показано выше, реализация средств точных вычислений достаточно проста и практически на любом языке можно самостоятельно создать свой аппарат такой обработки. Например, в книге [4] приводится пример организации вычислений со «сверхточностью» и в «сверхдиапазоне». Процессоры архитектуры IA-32 даже имеют специальные команды, облегчающие арифметические вычисления без округлений. Правда в 64-разрядном режиме используемая для этой цели пара команд DAA/DAS становится недоступной, однако это не сильно затруднит реализацию, поскольку такие команды несложно эмулировать программно, например:
;--------------- ЭМУЛЯЦИЯ DAA, ЗАПРЕЩЕННОЙ В РЕЖИМЕ X86-64 ------------------
PUBLIC DAA_X86_64:
PUSH RDX,RAX
LAHF
MOV EDX,EAX ;OLD CF И OLD AL
AND AH,NOT 1B ;СБРОСИЛИ CF
;---- ОБРАБОТКА МЛАДШЕЙ ТЕТРАДЫ ----
TEST AH,10000B ;ЕСЛИ ЕСТЬ AF
JNZ @
PUSH RAX
AND AL,0FH
CMP AL,9 ;ИЛИ ЕСЛИ ЦИФРА БОЛЬШЕ 9
POP RAX
JBE M2270
@: ADD AL,6 ;КОРРЕКЦИЯ ЦИФРЫ
OR AH,10000B ;УСТАНАВЛИВАЕМ AF
;---- ОБРАБОТКА СТАРШЕЙ ТЕТРАДЫ ----
M2270:TEST DH,1B ;ЕСЛИ СТОЯЛ OLD CF
JNZ @
CMP DL,99H ;ИЛИ НУЖЕН ПЕРЕНОС
JBE M2271
@: OR AH,1B ;УСТАНАВЛИВАЕМ CF
ADD AL,60H ;КОРРЕКЦИЯ ТЕТРАДЫ
;---- ПИШЕМ ГОТОВЫЙ БАЙТ И ВОССТАНАВЛИВАЕМ РЕГИСТРЫ И ФЛАГИ ----
M2271:SAHF
MOV [RSP],AL
POP RAX,RDX
RETОсновой точных вычислений является точное представление чисел в памяти компьютера. Двоично-десятичное представление позволяет легко организовать точные вычисления для чисел любой длины, т.е. любой точности. Проверено на практике, что для большинства экономических расчетов вполне хватает длины в 15 десятичных разрядов.
Литература
1. Д.Р. Джадд «Работа с файлами». Издательство «Мир» Москва, 1975
2. http://msdn.microsoft.com/ru-ru/library/system.decimal.aspx
3. Д. Караваев «К вопросу о совершенствовании языка программирования». RSDN Magazine #4 2011
4. Л.Ф. Штернберг «Ошибки программирования и приемы работы на языке ПЛ/1», Москва «Машиностроение», 1993